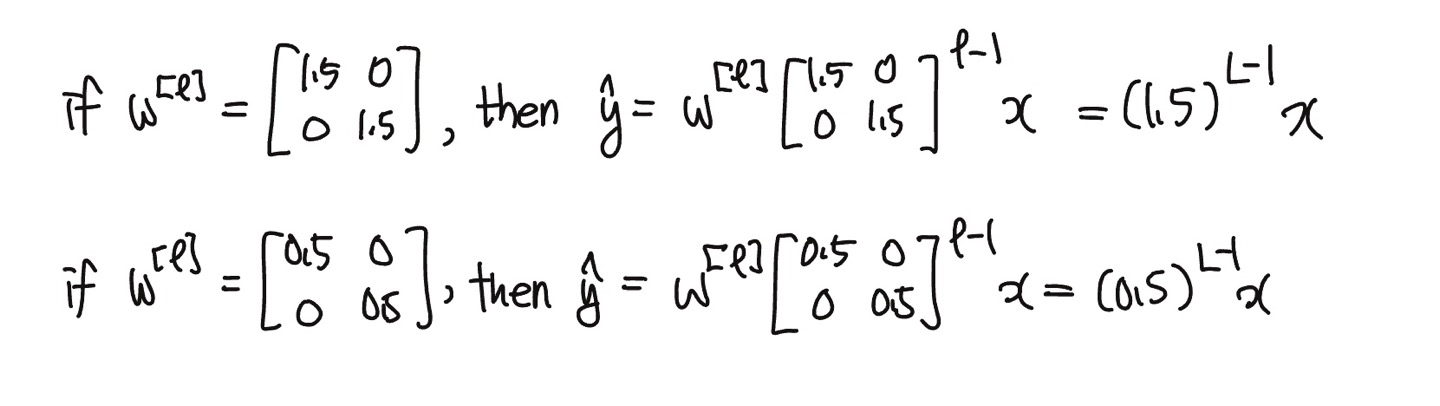07 최적화 문제 설정

boostcourse의 [딥러닝 2단계: 심층 신경망 성능 향상시키기] 강의를 수강 후 요약한 내용

입력값의 정규화

정규화 : 신경망을 빠르게 하는 방법

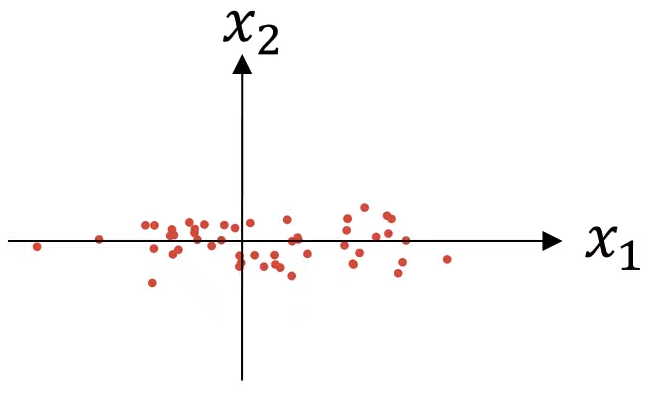
평균을 빼는 것

• 0의 평균을 갖게 될 때까지 훈련 세트를 이동하는
  • $\mu = \frac{1}{m} \sum_{i=1}^m x^{(i)}$
  • $x :=x-\mu$

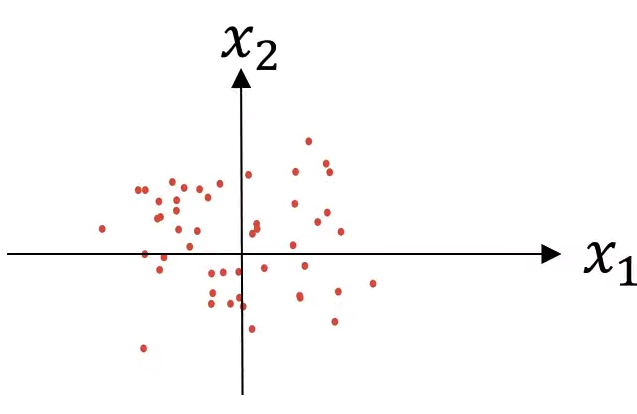
분산을 정규화하는 것

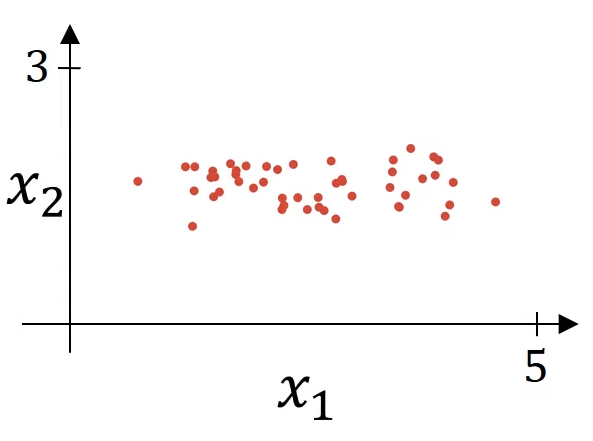
• 특성 $x1$이 특성 $x2$ 보다 더 높은 분산을 갖는다는 것을 알 수 있다.
  • $\sigma^2 = \frac{1}{m}\sum_{i=1}^m x^{(i)} \circ 2$
    • $\sigma$는 각 특성의 분산에 대한 벡터
  • $x:=\frac{x}{\sigma^2}$

이렇게 한다면, $x1$와 $x2$의 분산이 모두 $1$이 된다.

만약 이 방법을 훈련 데이터를 확대하는데 사용한다면, 테스트 테스를 정규화할 때도 같은 $\mu$와 $\sigma$를 사용해준다.

훈련 샘플과 테스트 샘플 모두 같은 값으로 정규화되어야한다.

평균을 0으로, 분산을 1로 만들어준다.

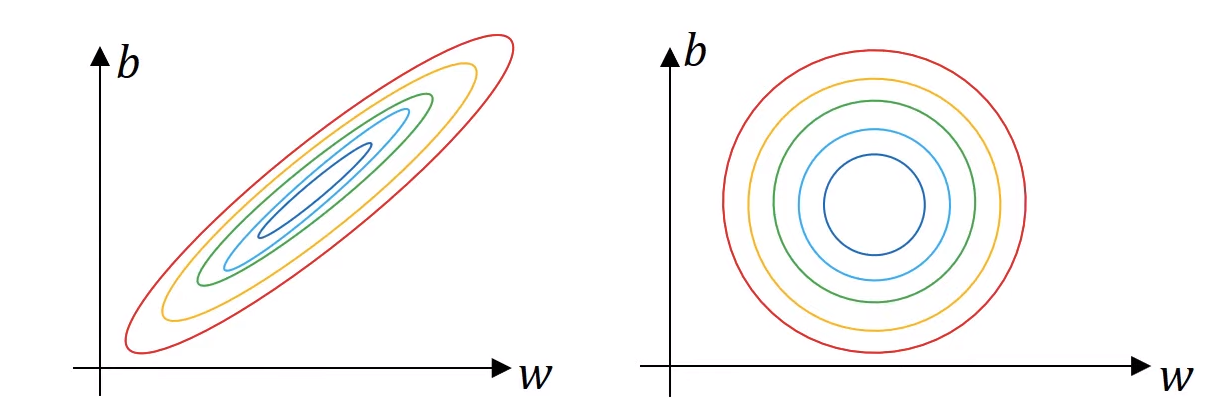
그렇다면 입력 특성들을 왜 정규화를 시켜야하나?

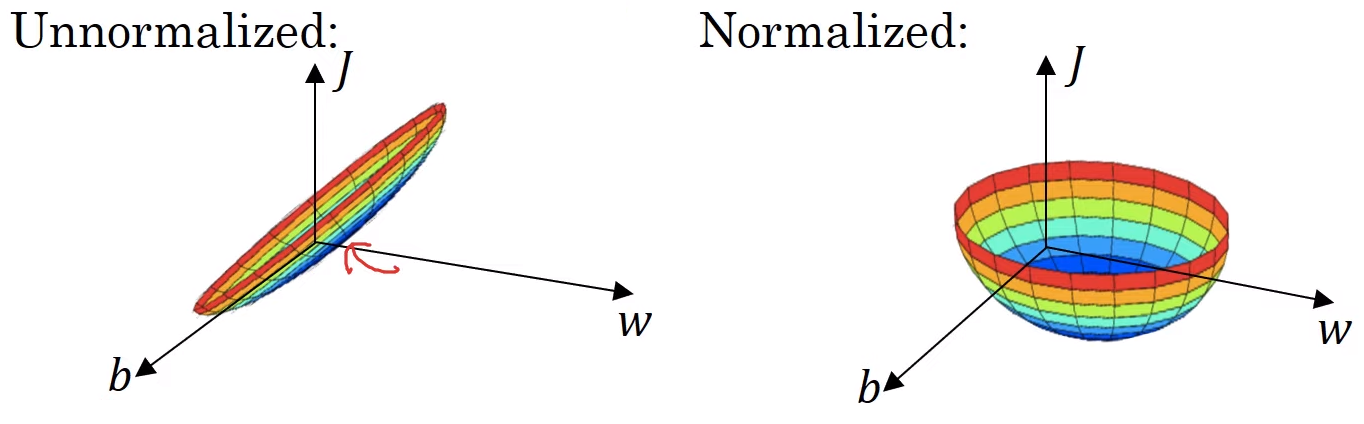
만약 정규화되지 않은 입력특성으로 비용함수를 계산하게 된다면, 이렇게 구부러진 활처럼 가늘고 긴 모양의 비용함수가 나오게 된다.

만약 정규화하지 않는다면, 각 $x$들의 scale이 다르다. 예를 들어, $x1 = { 1, …, 1000 }$이고, $x2= {0, …, 1 }$이라면, 위 형태의 가늘고 긴 모양의 비용함수가 나오게 된다. 그렇게 된다면, 매우 작은 학습률을 사용하고, 앞뒤로 왔다갔다 하기 위해 더 많은 단계가 필요하게 된다.

하지만 만약 정규화를 시켜준다면, 더 대칭의 형태를 갖는 비용함수를 구할 수 있게 되고, 그렇게 된다면 더 빠르게 경사 하강법을 계산하여 최소값을 구할 수 있게 될 것이다.

💡 특성들이 비슷한 크기를 가질 때, 비용함수가 더 둥글고 최적화하기 쉬운 모습이 된다.

경사의 소실과 폭발

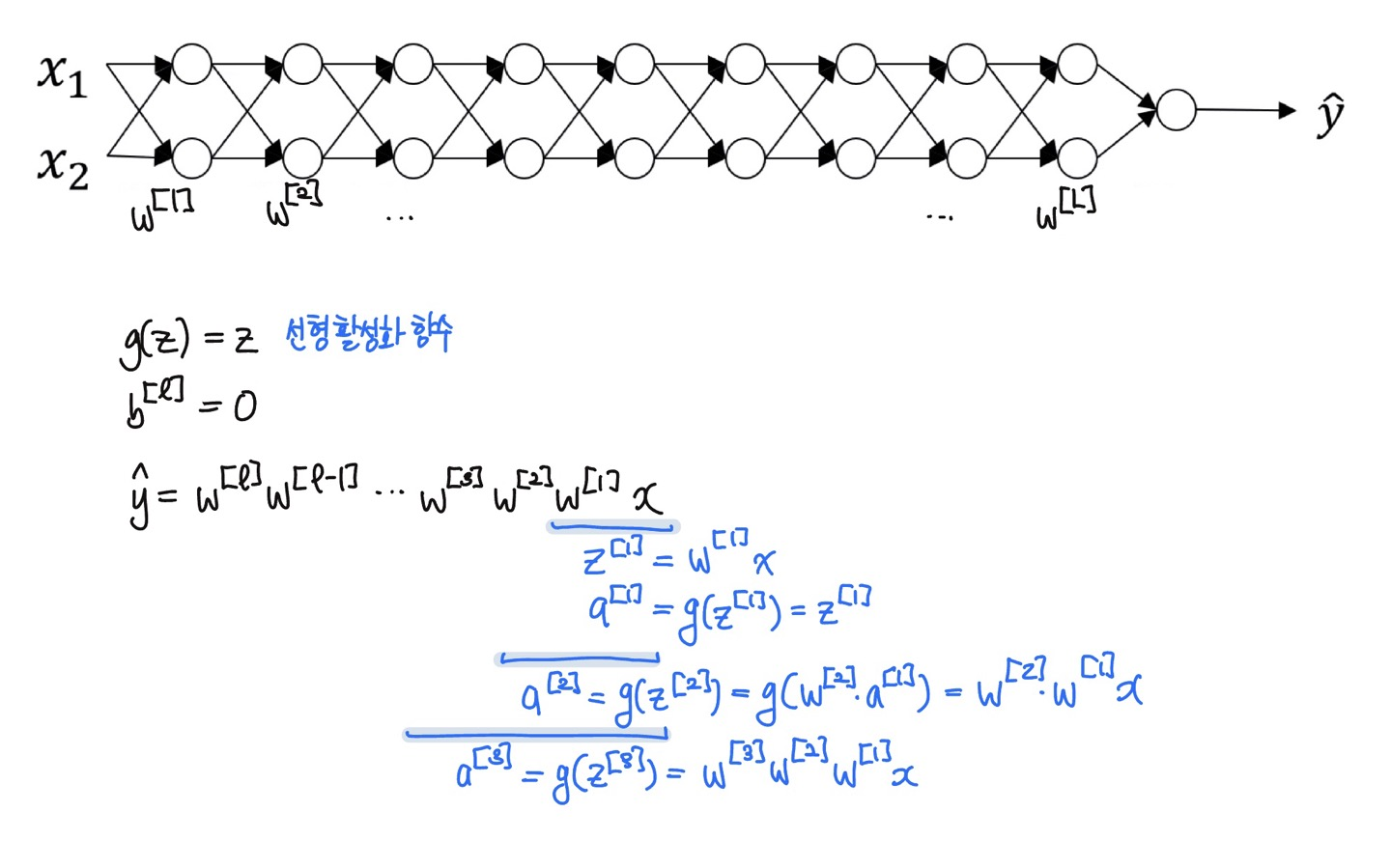
신경망이 깊어질 수록, 미분값/기울기가 아주 작아지거나 커질 수 있다. 이걸 경사의 소실 또는 폭발이라고 한다. 만약 기하급수적으로 작아진다면, 훈련 자체를 어렵게할 수 있다.

만약 $w^{[l]}$의 값이 1보다 조금 큰 값이고 $L$이 매우 큰 값이라면 (즉, 더 깊은 신경망일수록), $\hat{y}$은 기하급수적으로 커질 것이고, 만약 1보다 작은 값이라면 $\hat{y}$ 값이 기하급수적으 작아질 것이다. (현대의 신경망들은 대부분 150개의 층을 갖는다.)

$w > 1$ : 경사의 소실 $w < 1$ : 경사의 폭팔

💡 $w^{[l]}$값이 단위행렬(identity matrix : 주각대선의 원소가 모두 1이며, 나머지 원소가 모두 0인 정사각 행렬)보다 큰 값이라면 경사의 폭발, $w^{[l]}$값이 단위행렬보다 작은 값이라면 경사의 소실이 생긴다.

심층 신경망의 가중치 초기화

경사의 폭발이나 소실을 완전하게 해결할 수는 없지만, 많은 도움을 주는 해결법은 신경망에 대한 무작위의 초기화를 더 신중하게 선택하는 것이다.

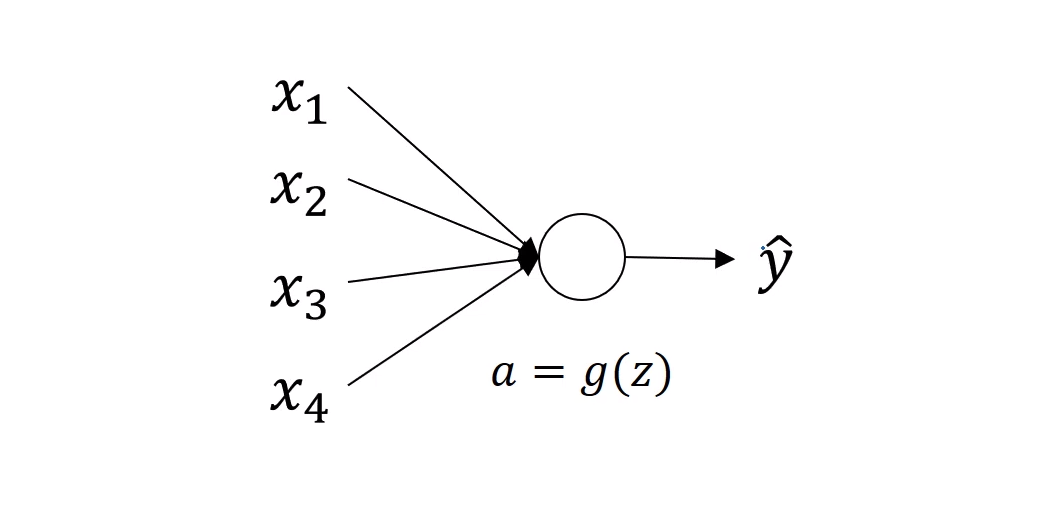
우선 단일 뉴런에 대한 예제를 알아보자.

z = w1x1 + w2z2 + ... + wnxn

$z$의 값이 너무 크거나 작아지지 않기 위해서는, $n$의 값이 클수록 $w$값이 작아져야한다.

$w$값을 작아지게 하기 위해서는 $w$의 분산을 $\frac{1}{n}$ 값으로 설정해주면 된다.

만약 ReLU 활성화 함수를 사용한다면, $w$의 분산을 $\frac{2}{n}$으로 설정해준다.

w[l] = np.random.randn(w.shape) + np.sqrt(2/n[l-1])

경사의 폭발이나 소실을 완전히 해결하지는 못하지만, 각각의 가중치 행렬 $w$값을 $1$보다 너무 커지거나 작아지지 않게 설정하여 너무 빨리 폭발하거나 소실하지 않게 한다.

만약 ReLU가 아닌 tanh 활성화 함수를 사용한다면, 세이비어 초기화 xavier initialization, $\sqrt{\frac{1}{n^{[l-1]}}}$ 또는 $\sqrt{\frac{2}{n^{[l-1]}+n^{[l]}}}$으로 $w$의 분산을 설정해준다.

이 모든 식들은 가중치 행렬 초기화를 위한 시작점을 제공한다. 이와 같은 분산을 원한다면 분산 매개변수는 또 다른 하이퍼파라미터가 된다. 가끔 이 하이퍼파라미터를 조정하는 것이 도움이 될 때가 있지만, 다른 하이퍼파라미터를 튜닝하는 것에 비해 중요한 것은 아니라고 한다.

경사 검사

💡 경사 검사는 경사 하강법을 통해 계산한 기울기, 즉 $d\theta$와 근사오차 $d\theta_{approx}$를 비교(=유클리드 거리 계산을 통해)해서 경사 하강법이 정상적으로 작동하였는지 확인하는 것이다.

기울기의 수치 근사

경사 검사를 통해 역전파를 맞게 구현했는지 확인할 수 있다. 경사 검사를 하기 위해서는 경사의 계산을 수치적으로 근사하는 방법을 알아보자

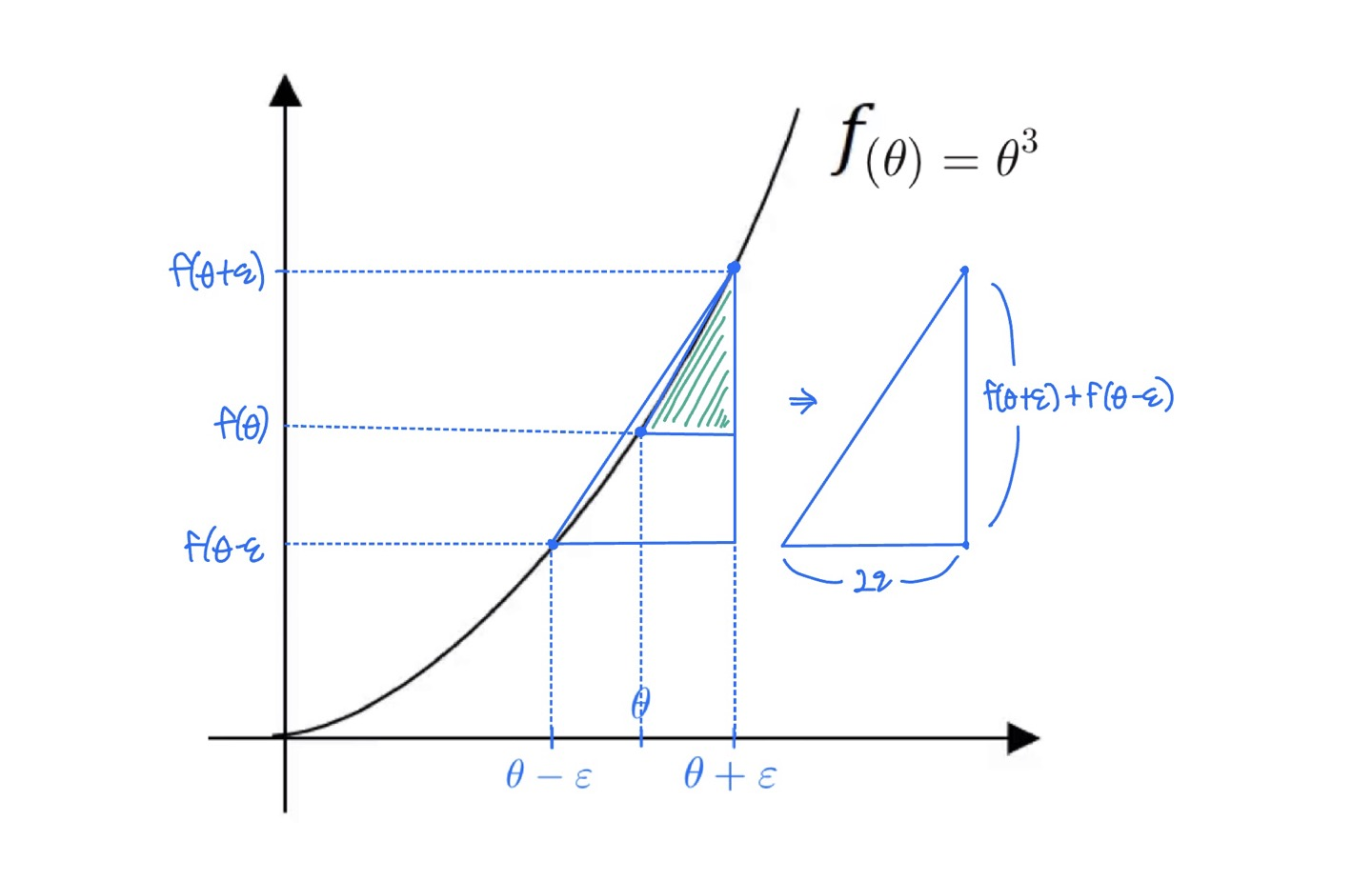
• 더 작은 초록색 삼각형의 넓이를 구하는 것보타, 더 큰 삼각형의 넓이를 구하는 것이 기울기의 수치를 근하는데 더 효과적이다.
• 이 큰 삼각형은 마치 2개의 작은 삼각형들을 고려하는 것과 같다. 즉, 한쪽만의 차이를 사용하지 않고 양쪽의 차이를 이용한다.

큰 삼각형의 넓이

\[\frac{f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon} \approx g(\theta)\] \[\frac{(0.01)^3 - (0.99)^3}{0.02} = 3.0001 \approx 3\] \[g(\theta) = 3\theta^2 = 3\]

• 근사 오차 approximate error = $0.001$
• 만약 한쪽 차이인 $\theta+\epsilon$ 만 사용했을 때는 근사오차가 $3.0301$이고 오차가 $0.03$이 되었다.

도함수의 공식적인 정의는 아래와 같다.

\[f'(\theta) = \lim_{\varepsilon \rightarrow 0} \frac{f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}\]

그렇다면 $0$이 아닌 $\varepsilon$ 값에 대해서 근사 오차는 $O(\varepsilon^2)$이다.

하지만 만약 작은 삼각형, 즉 한쪽의 차이만 고려한다면 이 값이 아닌 $\frac{f(\theta+\varepsilon)-f(\theta)}{\varepsilon}$으로 계산하는 것이데, 이렇게 된다면 근사 오차는 $O(\varepsilon)$이 된다.

이 빅오노테이션은 안에 있는 값에 상수를 곱해준다는 것인데, 매우 작은 값인 $\varepsilon$을 제곱하는것이 그냥 $\varepsilon$보다 더 작은 값이 될 것이다.

• 예를 들어 $\varepsilon=0.01$ 이라면, 각각의 근사오차는 $O(\varepsilon^2)=0.0001$이 되고 $O(\varepsilon)=0.01$이 될 것이므로, 근사 오차가 더 줄어드는 양쪽 차이를 사용하는 것이 더 정확하다.

경사 검사의 구현

• 경사 검사를 위해서 $W^{[1]}, b^{[1]}, …, W^{[L]}, b^{[L]}$의 차원을 변경하여 하나의 벡터 $\theta$로 연결한다. (concatenate)
• 그래서 비용함수 $J(W^{[1]}, b^{[1]}, …, W^{[L]}, b^{[L]})$가 $W$와 $b$에 대한 함수가 아닌, $\theta$에 대한 함수 $J(\theta)$로 바뀐다.
• 역전파의 도함수들 $dW^{[1]}, db^{[1]}, …, dW^{[L]}, db^{[L]}$를 같은 방법으로 차원을 바꿔 (reshape) 하나의 벡터 $d\theta$로 바꿔준다.
• 여기서 중요한 질문은 : $d\theta$가 과연 $J(\theta)$의 기울기인가? (=맞게 계산 되었는가? 역전파에서의 계산 오류는 없었는가?)

구현 방법

$J(\theta) = J(\theta_1, \theta_2, \theta_3, …)$으로 확장시키는 것이 가능하다. 그렇기 때문에 경사 검사를 구현하기 위해 loop를 사용한다.

for each i :

$d\theta_{approx} [i] = \frac{J(\theta_1, \theta_2, …, \theta_i + \varepsilon, …) - J(\theta_1, \theta_2, …, \theta_i - \varepsilon, …)}{2\varepsilon} \approx d\theta[i] =\frac{\partial J}{\partial \theta_i}$

이 $d\theta_{approx}$, 즉 근사 오차 값을 모든 $i$에 대해 계산하면, 이 근사오차의 차원과 도함수 $d\theta$의 차원이 $\theta$의 차원과 같게 될 것이다. 그리고 이제 이 두 값이 근사적으로 같은지 확인해야한다.

유클리드 거리를 통해 이 두 벡터가 근서적으로 같은지 정의할 수 있다.

\[\frac{||d\theta_{approx} - d\theta||_2}{||d\theta_{approx} + d\theta||_2}\]

분모는 위 벡터를 정규화 시켜주고, 또 분자의 벡터가 아주 크거나 작을 때를 대비해 이 식을 비율로 바꿔준다.

실제로 구현할 때, $\varepsilon=10^{-7}$으로 설정해준다. 그리고 이 범위에서의 유클리드 거리가

• $10^{-7}$이거나 더 작은 값이 나온다면 잘 근사되었을 것이다.
• $10^{-5}$이면 좋을 가능성이 크지만 벡터의 원소의 크기를 한번 더 확인해 너무 큰 값이 없는지, 원소들의 차이가 너무 크지 않은지 확인할 필요가 있을 것이다.
• $10^{-3}$이거나 더 큰 값이 나오면 버그가 있을 가능성이 매우 크기 때문에 $\theta$의 개별적인 원소들을 확인해서 근사오차와 도함수의 차이가 심한 원소를 추적해서 미분의 계산이 잘못되지 않았는지 확인해야할 것이다.

경사 검사 구현을 위해 주의할 점

1. 훈련에서 경사 검사를 사용하지 않고 디버깅을 위해서만 사용한다.
   • 모든 $i$에 대해 계산하는 것은 너무 느릴 수 있다.
2. 만약 경사 검사의 알고리즘이 실패 했다면, 어느 원소 부분에서 실패했는지를 확인하여 버그를 확인한다.
   • 만약 근사오차와 도함수의 차이가 크게 나왔다면, 각 원소들을 확인해 큰 차이가 나게 하는 원소가 무엇인지를 확인해본다. 역전파에서 해당 원소의 도함수 계산이 잘못되었을 가능성이 크다.
3. 정규화를 하는 것을 잊으면 안된다.
4. 경사 검사는 드롭아웃과 같이 적용할 수 없다.
   • 드롭아웃을 사용할 때는 명확한 $J$를 계산할 수 없다. 비용함수 $J$는 어떤 반복에서든지 삭제될 수 있는 기하급수적으로 큰 노드의 부분집합으로 정의된다. 만약 드롭아웃을 사용하면 매번 다른 부분집합의 노드를 랜덤하게 삭제하기 때문에 비용함수 $J$를 계산하는 것이 매우 어려워진다.
   • 그렇기 때문에 드롭아웃을 하지 않고 알고리즘이 작동하는지 우선 확인하고 드롭아웃을 켜는 방법을 사용해야한다.
5. 흔한 일은 아니지만, 랜덤 초기화에서의 $W$와 $b$가 0에 가까울 때 경사 하강법의 구현이 맞게 된 경우가 있다.
   • 이 경우 경사 하강법이 진행될 수록 오차가 커질 수 있다. 이런다면 경사 하강법이 0에 가까울 때만 맞는 것일 수도 있다.
   • 이런 경우 랜덤 초기화에서 경사 검사를 진행하고, 훈련을 조금 더 시킨 후 경사 검사를 다시 해보는 방법이 있다.