06 신경망 네트워크의 정규화
Boostcourse의 [딥러닝 2단계 심층 신경망 성능 향상시키기] 2강 강의 요약
boostcourse의 [딥러닝 2단계: 심층 신경망 성능 향상시키기] 강의를 수강 후 요약한 내용
정규화 (1) $L_2$ Regularization (2) Dropout Regularization (3) Data Augmentation (4) Early Stopping
$L_2$ 정규화
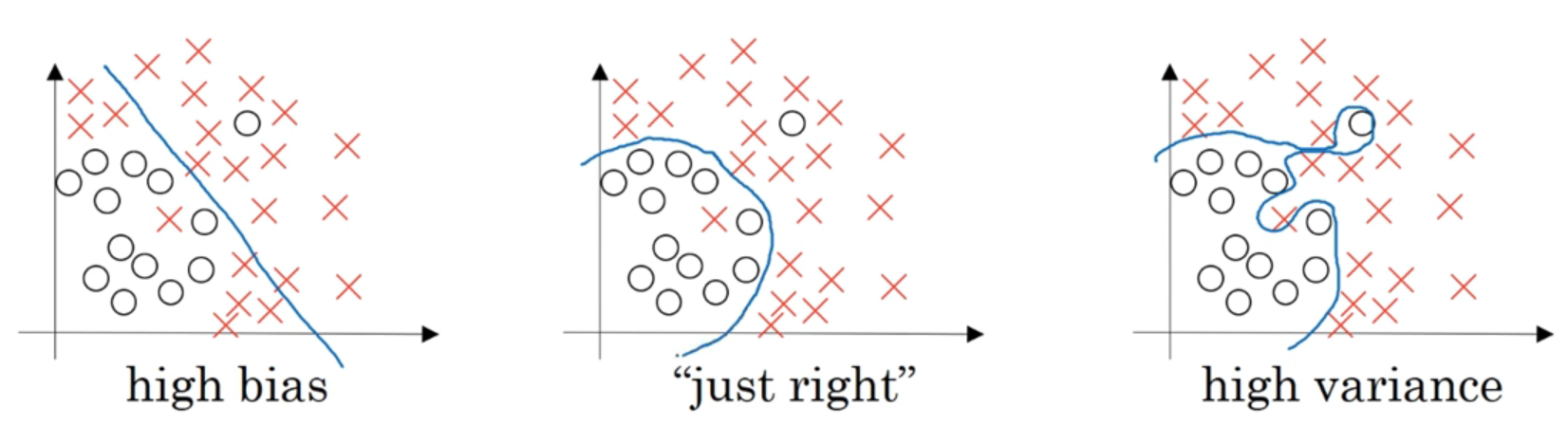
정규화를 추가하는 것은 과대적합을 줄이고 분산을 줄이는데 도움이 된다.
로지스틱 회귀의 정규화
로지스틱 회귀는 아래의 비용함수 $J$를 최소화하는 것! $\quad$ - 훈련 샘플의 개별적인 예측의 손실에 관한 함수 $\quad$ - $w, b$는 매개변수
로지스틱 회귀를 정규화하기 위해서는 정규화 매개변수라고 하는 $\lambda$를 추가해야한다.
\[J(w,b)=\frac{1}{m}\sum_{i=1}^mL(\hat{y^{(i)}}, y^{(i)}) + \frac{\lambda}{2m}||w||_2^2\]$L_1$ Regularization
$\frac{\lambda}{2m}\sum_{j=1}^{n_x} w_j = \frac{\lambda}{2m} w _1$ - 만약 $L_1$ Regularization을 사용한다면 $w$가 희소(= 안에 0이 많아진다)해진다. 어떤 사람들은 $L_2$ 정규화가 메모리를 적게 사용하기 때문에 모델을 압축하는데 도움이 된다고 하는데, 이것은 모델의 성능에 크게 도움이 되지 않는다.
- 만약 모델을 압축하는 것이 목적이라면 $L_1$ 정규화 효과적일 것
- 정규화를 위해서는 $L_2$ 정규화를 사용한다
$L_2$ Regularization
$ w ^22 = \sum{j=1}^{n_x}w_j^2 = w^Tw$ - $\frac{\lambda}{2m}b^2$도 더해줄 수 있지만, 보통은 생략한다. 높은 분산을 갖는 모델들은 $w$가 많은 매개변수가 있고, $b$는 하나의 실수이기 때문에 단 하나의 매개변수이다. 그래서 이 하나를 더해주는 것이 모델에 큰 변화를 주지 않기 때문에 굳이 추가할 필요는 없는 것이다.
정규화 매개변수 : $\lambda$
- 개발 세트 혹은 교차 검증 세트에서 다양한 값을 시도해서 훈련 세트와 잘 맞으면서 두 매개변수의 노름을 잘 설정해서 과대적합을 막을 수 있는 최적의 값을 찾는 것
- 설정이 필요한 다른 하이퍼파라미터이다
신경망의 정규화
\[J(w^{[1]}, b^{[1]}, ... , w^{[l]}, b^{[l]}) = \frac{1}{m}\sum_{i=1}^mL(\hat{y^{(i)}}, y^{(i)}) + \frac{\lambda}{2m}\sum^L_{l=1}||w^{[l]}||^2_F\]Frobenius Norm (프로베니우스 노름)
$ w^{[l]} ^2F = \sum{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}} (w_{ij}^{[l]})^2$ - $w : (n^{[l]}, n^{[l-1]})$
- 행열의 원소 제곱의 합이라는
정규화를 하기 전에는 $dw$를 계산하고, $w^{[l]} := w^{[l]} - \alpha dw^{[l]}$을 통해 $w$를 업데이트한다.
- $dw =$ $dz^{[l]} \times a^{[l-1]}$ ← 역전파에서 구한
- $w^{[l]} := w^{[l]} - \alpha dw^{[l]}$
만약 정규화 항을 더해주게 된다면 람다값을 추가한 $dw$로 $w$를 계산한다
- $dw^{[l]} = dz^{[l]} \times a^{[l-1]} \space +$ $\frac{\lambda}{m}w^{[l]}$
- $w^{[l]} := w^{[l]} - \alpha dw^{[l]}$
Weight Decay (가중치 감쇠)
$w$를 계산하는 식을 풀어쓴다면,
$w^{[l]} := w^{[l]} - \alpha [(backpropagation) + \frac{\lambda}{m}w^{[l]}$
$\qquad = w^{[l]}$ $- \space \frac{\alpha\lambda}{m}w^{[l]}$ $- \space \alpha(backpropagation)$
$\qquad= w^{[l]}($ $1 - \frac{\alpha\lambda}{m}w^{[l]}$$) -\alpha(backpropagation)$
즉, 행렬 $w^{[l]}$에서 $\frac{\alpha\lambda}{m}w^{[l]}$만큼을 빼준 것이기 때문에 이 값은 계속 감소하게 된다.
💡 가중치 행렬 $w$에 1보다 조금 작은 값인 $(1 - \frac{\alpha\lambda}{m}w^{[l]})$를 곱해주기 때문에 $L_2$ 정규화는 weight decay라고 부르는 것이다.
어떻게 $L_2$ 정규화가 과대적합을 줄일 수 있나?
| $J(w^{[l]}, b^{[l]}) = \frac{1}{m}\sum_{i=1}^mL(\hat{y^{(i)}}, y^{(i)}) + \frac{\lambda}{2m}\sum^L_{l=1} | w^{[l]} | ^2_F$ |
- 만약 $\lambda$가 커진다면, $w^{[l]}$가 0에 가까워질 것
- 즉, 은닉 유닛의 영양력을 0에 가깝게 줄이면서, 로지스틱 회귀에 가까운, 더 간단한 네트워크로 만들어주는 것
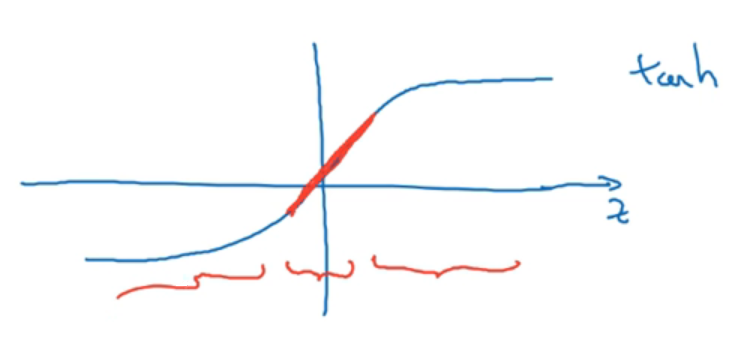
위 activation 함수 $\tanh$를 사용한다고 해보자.
이 함수는 만약 $z$값이 작으면 결과값이 선형에 가까운 값으로 나오게 된다.
그렇기 때문에 만약 $\lambda$가 커지고 $w^{[l]}$가 작아지면
- $z^{[l]} = w^{[l]}a^{[l-1]} + b^{[l]}$
- $z$값이 작아질 것, 즉 작은 범위의 값(그래프에서 빨갛게 표시된 부분)을 갖게 될 것이다.
- $g(z)$이 거의 1차원 함수가 될 것이다.
그래서 아무리 깊은 신경망이라도, 또는 층이 선형회귀처럼 직선의 함수를 갖게 되고, 모든 층이 선형이면 전체 네트워크가 선형 신경망이 된다.
그렇기에 매우 복잡한 계산, 위 사진의 ‘높은 분산’ 갖는 자세한 계산을 불가능하게 만든다.
- 모델이 더 간단해지는 것
드롭아웃 정규화
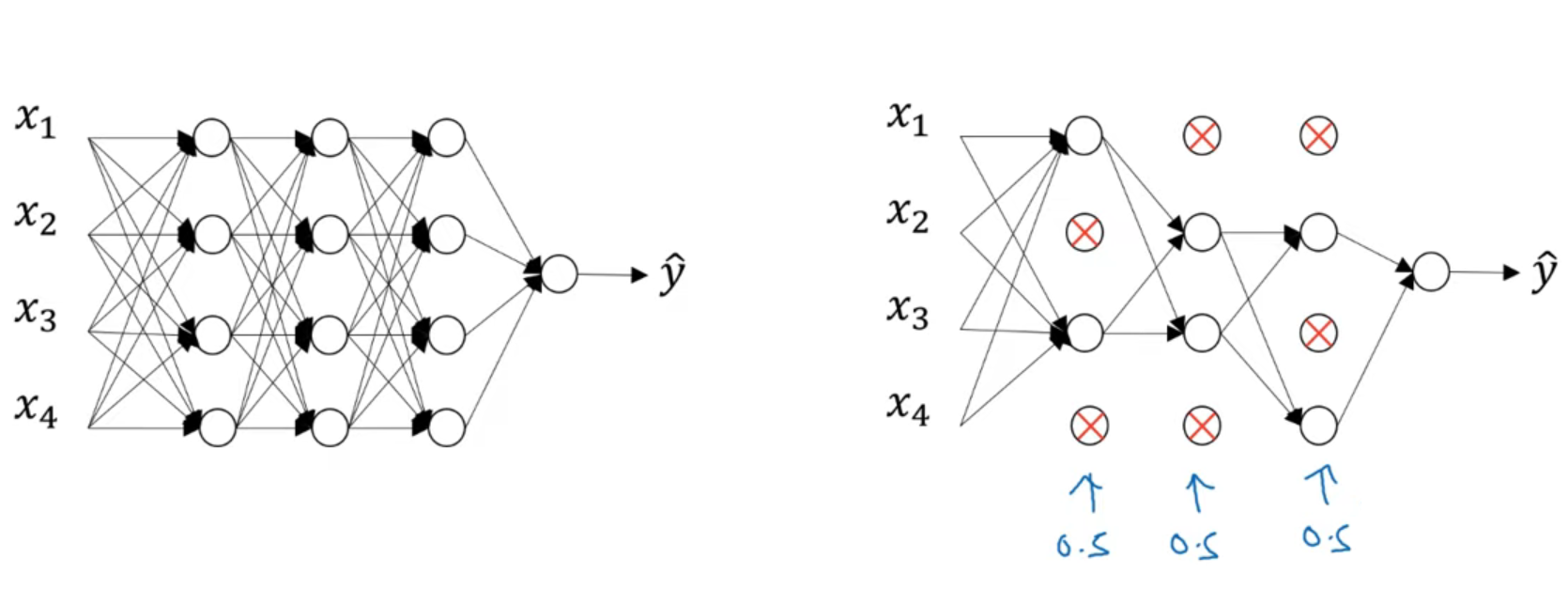
신겨망 각각의층에 대해 노드를 삭제할 확률을 결정하는 것
만약 왼쪽의 모델의 각 층의 노드를 삭제할 확률이 $0.5$라면, 하나의 훈련 샘플에 대해서 노드를 삭제하고 그 노드들에 링크를 다 끊은 후 역전파로 훈련시킨다. 다음 훈련 샘플을 훈련 시킬 때는 또 다른 노드들을 삭제하고 링크를 끊은 후 역전파로 훈련시킨다.
즉, 각 훈련을 더 간단한 모델에서 진행하는 것과 같이 하여 정규화를 진행하는 것
Inverted Dropout 역 드롭아웃
역 드롭아웃은 노드를 삭제후에 얻은 활성화 값 a에 keep.prop을 나눠 주는 것
1
2
keep.prob = 0.8 # 노드들을 0.8에 확률로 삭제시킬 것
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep.prob
d3은 어떤 노드를 삭제시킬지 랜덤하게 결정해주는 것np.random.rand이 (0,1)사이의 값을 랜덤하게 만들어주고,< keep.prob을 통해 T/F값으로 변환해준다- 이 T/F 행렬을
a3에 곱해주면서 F값들을 없애준다 (F=0)
1
2
a3 = np.multiply(a3,d3) # a3 *= d3
a3 /= keep.prob # a3의 기댓값을 동일하게 유지시킬 수 있게하는 역드롭아웃 기법
0.2만큼의 값이 삭제되었기 때문에 이 값을 마지막에a3을keep.prob인0.8로 나눠줌으로서 기존에 삭제하지 않았을 때 활성화 값z4의 기대값와 같게 기대값을 유지시키는 것이다.
왜 드롭아웃이 효과적인가?
- 드롭아웃에서는 입력 노드들이 랜덤하게 삭제되기 때문에 한 노드가 특정 입력에 유난히 큰 가중치를 부여하기 어렵다.
- 그래서 입력 노드들의 가중치를 분산시킨다
- 만약 가중치가 분산되면, 가중치의 노름의 제곱값이 줄어들게된다.
- 가중치의 노름의 제곱값이 줄어든다면, $L_2$ 정규화의 효과처럼 과대적합을 막는데 도움이 된다
$L_2$ 정규화랑 다른 점이라면, 그 가중치에 곱해지는 활성화의 크기에 따라 다른 가중치는 다르게 취급한다.
- L2 regularization helps constrain weight values towards smaller magnitudes
- Dropouts act more like an ensemble method that allows stronger connections within neural nets via random dropouts that enable better feature selection throughout various datasets for improved accuracy gains when predicting new data points outside its original train set boundaries- ultimately reducing excessive complexity with increased efficiency costs associated with parameter tuning / optimization processes inherent within deep learning architectures themselves making them ideal tools applicable across various machine learning tasks — 출처
다른 정규화 방법들
Data Augmentation 데이터증식
더 많은 데이터를 넣으면 과대적합을 막는데 도움이 된다. 하지만 더 많은 데이터를 구하는 데는 현실적으로 어려울 때가 많다.
이미지 데이터의 경우, 같은 사진을 무작위로 편집해 하나의 데이터로 데이터 세트를 증가시키고 추가적인 가짜 이미지들을 생성해주는 것이다.
이렇게 데이터를 늘리는 것은 독립적인 데이터를 추가하는 것보다는 더 많은 정보를 추가해주지는 않지만, 비싸지 않게 데이터를 더 얻을 수 있는 방법이다.
또한 모델에게 회전하거나 확대한 이미지도 같은 물체 (예를 들면 고양이)라는 것을 학습시킬 수도 있다.
Early Stopping 조기종료
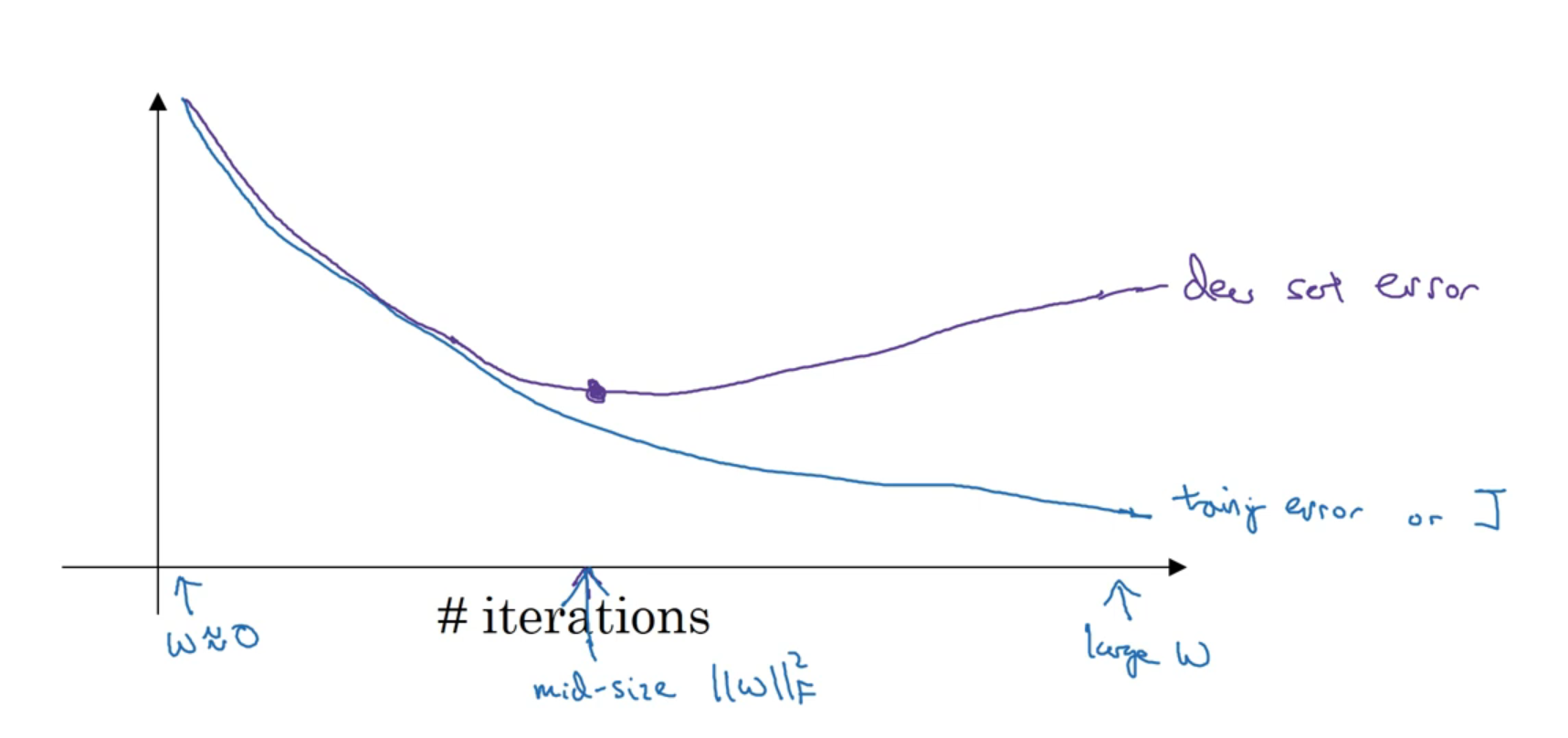
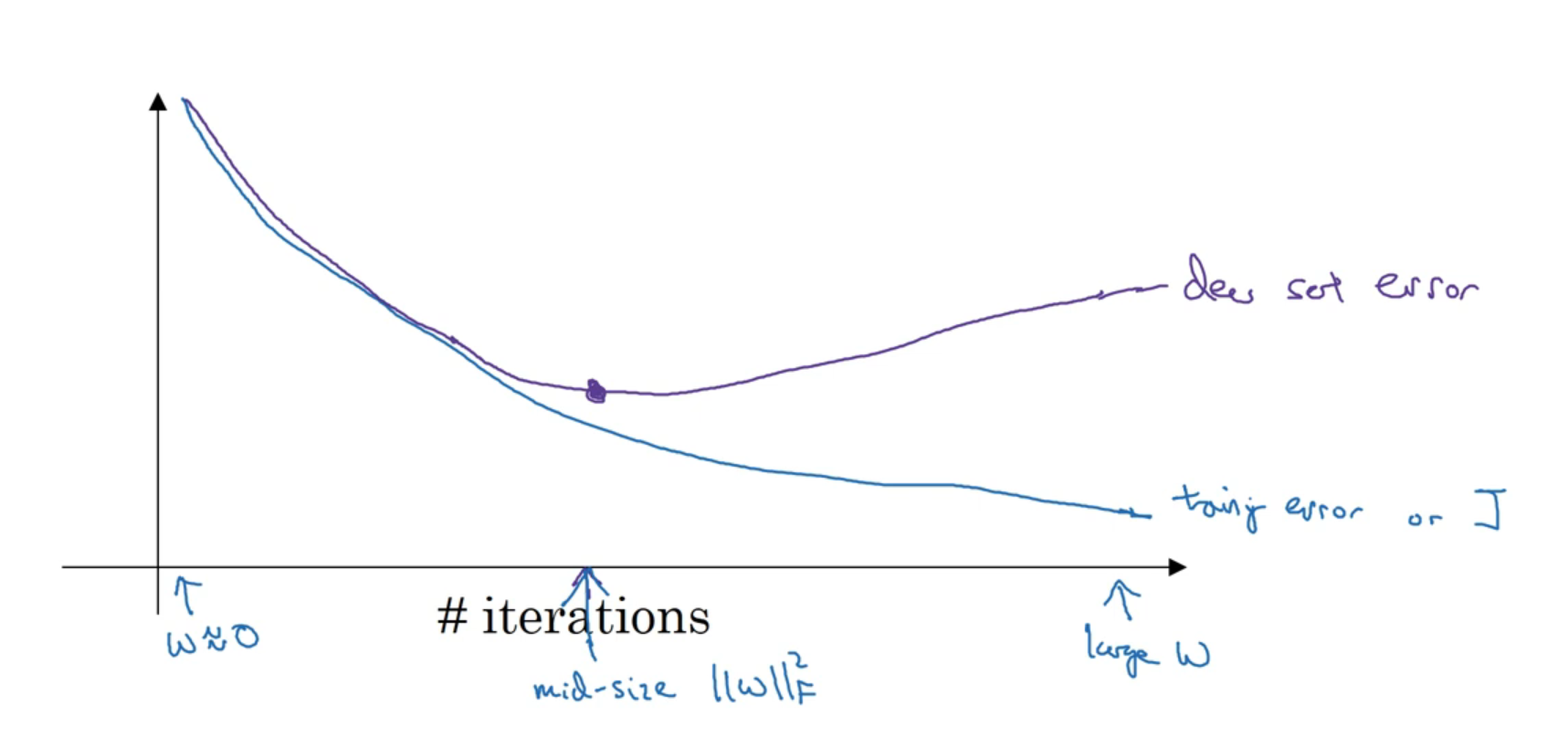
조기종료에서는 훈련세트에서의 오차를 확인하는 것 뿐만아니라, 개발 세트에서의 오차도 확인하며 모델을 훈련시킨다.
그래서 개발 세트에서 가장 효과적일 때에 모델을 조기에 종료시킨다.
이게 왜 효과적인가?
- 더 많은 실행을 할 수록 모델의 $w$값은 증가하게 된다.
- 앞서 정규화 방법론들을 보며 모델의 $w$값이 작아질 때에 모델이 더 간단해지며 과적합을 피할 수 있게 된다는 것을 확인했다.
- 그렇기 때문에 조기에 모델의 학습을 종료시켜 더 효과적인 모델을 만들 수 있게 되는 것이다.
조기종료의 단점
- 머신러닝은 (1) 비용함수 $J$를 최적화시키는 것과 (2) 과대적합을 막기 위한 방법론들이 진행한다. 머신러닝에서는 이미 많은 하이퍼파라미터들이 존재하기에 여러 알고리즘 중 하나를 선택하는 것이 어렵다.
- 그렇기 때문에 비용함수 $J$를 최적화하는 것에 집중하는 것, 즉 $J(w,b)$를 최소화하는 것에 집중하는 것이 모델을 더 간단하게 하는 방법일 수 있다. 그리고 과대적합을 막는 것은 완전히 별개의 일이며, 다른 도구들이 필요하다.
- 이 원리는 Orthogonalization 직교화라고 부르며, 하나 목적에 집중하는 것을 의미한다.
- 하지만 조기 종료의 경우, 이 두 가지 목적, 비용함수 $J$의 최소화와 과대적합을 막는 것,을 동시에 해결하려고 하기 때문에 이 두 문제를 독립적으로 해결할 수 없게 한다.
- 조기에 종료시킴으로서 비용함수의 최적화를 중단하며, 동시에 과대적합을 피하려고 하기 때문이고, 문제를 더 복잡하게 만들 수 있기 때문이다
대안
- 조기종료 대신 $L_2$ 정규화를 사용하는 것도 방법인데, 이 방법에 단점은 여러 $\lambda$ 값을 확인해야하기 때문에 컴퓨터 적으로 더 많은 비용이 들게 하는 것이다.
- 그렇기 때문에 조기 종료의 장점이라고 하면 더 적은 비용으로 빠르게 $w$ 값을 구할 수 있다는 것에 있다.