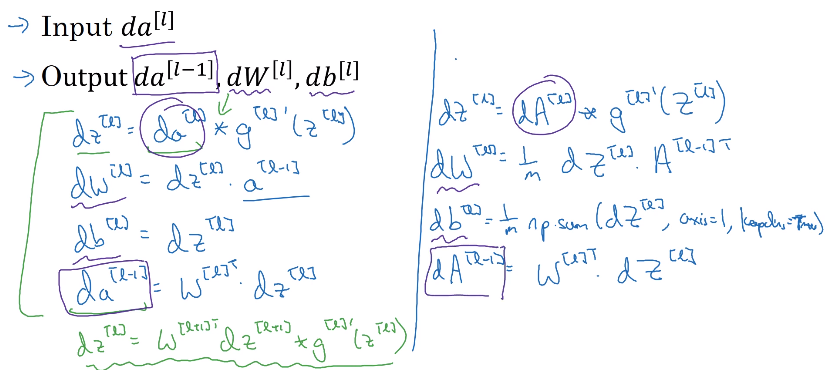04 심층 신경망 네트워크

boostcourse의 [딥러닝 1단계: 신경망과 딥러닝] 강의를 수강 후 요약한 내용

지금까지의 복습

• • 로지스틱 회귀 분석과 단일 은닉층을 가진 신경망의 순방향 전파와 역방향 전파
• 벡터화와 왜 랜덤하게 초기값을 초기화시켜야하는지

더 많은 층의 심층 신경

심층 신경망이란?

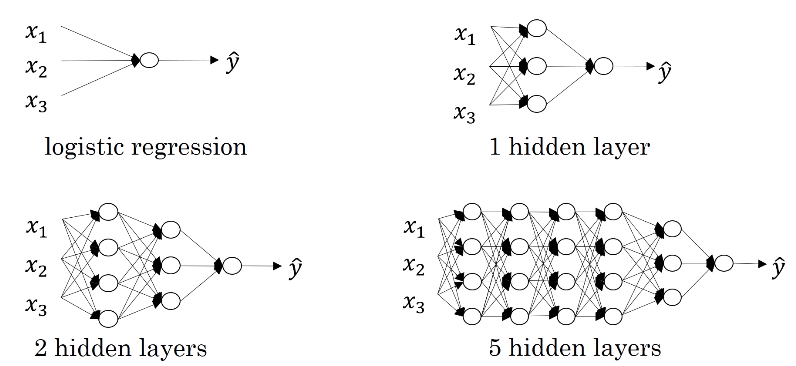
• 지금까지 배운 것은 로지스틱 신경망과 하나의 은닉층을 가진 신경망
• 로지스틱 신경망과 하나의 은닉층을 가진 신경망은 얕은 신경망이라고 한다
• 그동안 머신러닝 커뮤니티에서 더 깊은 신경망이 얕은 신경망은 할 수 없는 계산을 할 수 있다는 것을 알아냈다.
• 하지만 얼마나 깊은 신경망을 사용해야 하는지 미리 예측하기는 어렵다.

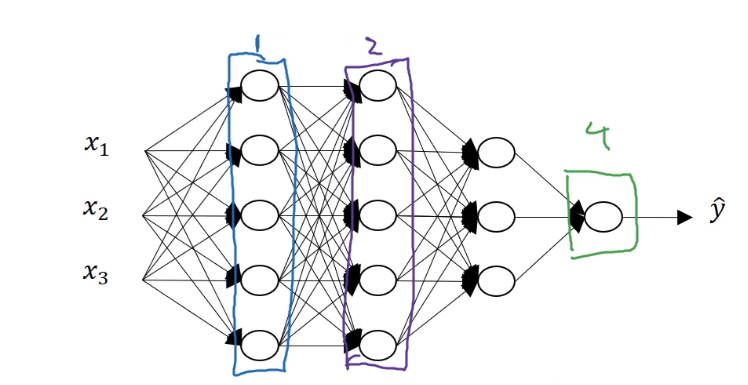
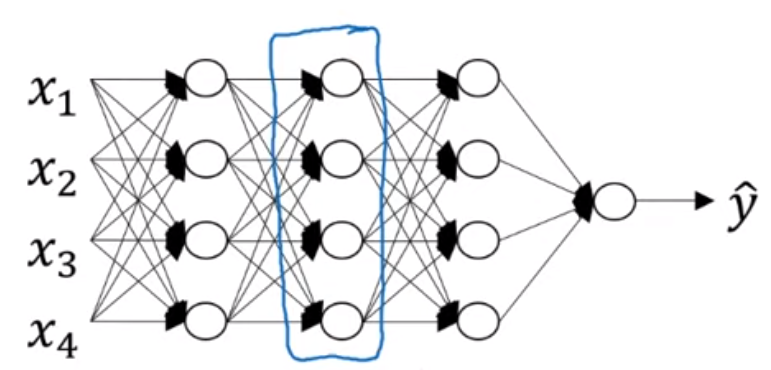
• 4개의 층, 3개의 은닉층, 그리고 $(5,5,3,1)$의 노드를 갖고 있는 신경망

• $L =$ number of layers in the network
  • $L=4$
• $n^{[l]} =$ number of nodes/units in layer $l$
  • $n^{[0]} = n_x = 3$
  • $n^{[1]} = 5$
  • $n^{[2]} = 5$
  • $n^{[3]} = 3$
  • $n^{[4]} = n^{[L]} = 1$
• $a^{[l]} =$ activation in layer $l$ (활성값)
• $a^{[l]} = g^{[l]}(z^{[l]})$
• $w^{[l]} =$ weights for $z^{[l]}$ (가중치 행열)

• $b^{[l]}$ = 벡터편향

• 입력 특징은 $X$라고도 불리며, 또한 $X = a^{[0]}$ 이다
• 마지막 층의 활성값인 $a^{[L]}=\hat{y}$이다.

심층 신경망에서의 정방향 전파

우선 단일 데이터에서의 정방향 전파를 알아보자

첫번째 레이어에서 계산되는 값이다

$z^{[1]} = W^{[1]}x + b^{[1]}$

• $x=a^{[0]}$이기 때문에, 위 식은 $z^{[1]} = W^{[1]}$$a^{[0]}$ $+ b^{[1]}$ 와 같다
• $W$와 $b$는 첫번째 층에서 활성화에 영향을 주는 파라미터들이다

$a^{[1]} = g^{[1]}(z^{[1]})$

두번째 레이어에서의 값들이다

$z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}$

$a^{[2]} = g^{[2]}(z^{[2]})$

세 번째 은닉층에서의 값들이다

• $z^{[3]} = W^{[3]}z^{[2]} + b^{[3]}$
• $a^{[3]} = g^{[3]}(z^{[3]})$

마지막 출력층에서의 값들이다

$z^{[4]} = W^{[4]}a^{[3]} + b^{[4]}$

$a^{[4]} = g^{[4]}(z^{[4]}) = \hat{y}$

즉, 각 은닉층에서 계산하는 값은 아래와 같다.

• $z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]}$
• $a^{[l]} = g^{[l]}(z^{[l]})$

위 식들을 벡터화하면 아래와 같다

첫번째 은닉층

$Z^{[1]} = W^{[1]}A^{[0]} + b^{[1]}$, where $X=A^{[0]}$

$A^{[1]} = g^{[1]}(Z^{[1]})$

두번째 은닉층

$Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$

$A^{[2]} = g^{[2]}(Z^{[2]})$

세 번쨰 은닉층

$Z^{[3]} = W^{[3]}A^{[2]} + b^{[3]}$

$A^{[3]} = g^{[3]}(Z^{[3]})$

마지막 출력층

$Z^{[4]} = W^{[4]}A^{[3]} + b^{[4]}$

$\hat{Y} = g^{[4]}(Z^{[4]}) = A^{[4]}$

• 이렇게 반복되는 식들을 보면, 같은 식들이 각 층에서 반복되기 때문에 for문을 사용해야한다
• 신경망은 for문의 사용을 최대한 피해야하지만, 이 경우 각 층들에서 반복할 수 있게 하는 방법은 for문을 제외한 마땅한 방법이 없기 때문에, 여기서는 for문을 사용해 반복시킨다.

행열의 차원을 알맞게 만들기

심층 신경망에서 에러를 피하기 위해서는 행렬 차원에 대해 체계적으로 생각해야한다.

$W^{[1]}$의 경우, 현재 층의 노드의 수와 전 층의 노드의 수의 차원을 갖고 있다.

• $W^{[1]} : (n^{[1]}, n^{[0]})$
• $W^{[l]} : (n^{[l]}, n^{[l-1]})$

$b^{[1]}$의 차원은 $W^{[1]}x$ 와 $z^{[1]}$의 차원과 같아야한다.

• $b^{[1]} : (n^{[1]}, 1)$
• $b^{[l]} : (n^{[l]}, 1)$

역방향 전파의 경우, $dW^{[l]}$는 $W^{[l]}$와, 그리고 $db^{[1]}$는 $b^{[1]}$와 같은 행열의 차원을 갖게 된다.

• $dW^{[l]} : (n^{[l]}, n^{[l-1]})$
• $db^{[l]} : (n^{[l]}, 1)$

또한 $a^{[l]}$값이 $z^{[l]}$를 활성화 함수에 넣어 만든 값이기 때문에 $z^{[l]}$와 $a^{[l]}$의 차원이 같아야한다.

• $a^{[l]} = g^{[l]}(z^{[l]})$ 이기 때문에 차원이 같아야 한다는 뜻
• $x=a^{[0]}$이라는 것을 까먹지 말기!
  • $x = a^{[0]}$는 $(n^{[0]},1)$이다.

💡 벡터화된 계산식들도 위 식들과 비슷하다. $W, b, dW,db$의 의차원은 같지만, $z, a, x$의 차원은 조금 달라진다.

$z^{[1]} = W^{[1]}x + b^{[1]}$

$\rightarrow Z^{[1]} = W^{[1]}X + b^{[1]}$

$z^{[l]}, a^{[l]} : (n^{[l]},1)$

$\rightarrow Z^{[l]}, A^{[l]} : (n^{[l]}, m)$

$dZ^{[l]}, dA^{[l]} : (n^{[l]}, m)$

$l=0$ 일 떄 $X=A^{[0]}$임을 기억해야한다.

• $A^{[0]} = X = (n^{[0]}, m)$

왜 심층 신경망이 더 많은 특징을 잡아 낼수 있을까?

심층 신경망의 계산

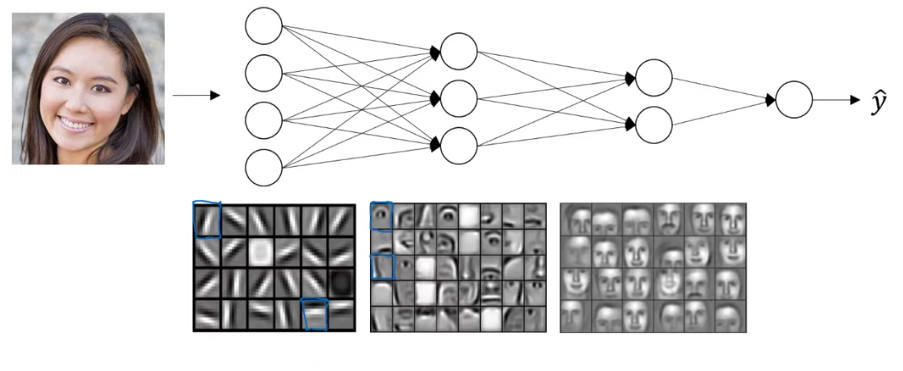
• 만약 얼굴 사진을 입력값으로 넣는다고 한다
• 그렇다면 첫번째 층은 특성 탐지기나 모서리 탐지기라고 할 수 있다.
  • 이 사진에서 20개의 은닉층은 20개의 작은 상자로 이루어져있다.
  • 즉 사진을 보고, 이 사진의 모서리가 어디있는지 알아보는 과정이다.
• 다음 층에서는, 여기서 감지된 모서리와 그룹화된 모서리들을 통해, 눈이나 코의 부분을 찾아내는 등, 얼굴의 일부를 감지할 수 있다.
• 다음 층에서는 이 얼굴의 일부를 통해 서로 다른 종류의 얼굴을 감지해낼 수 있게 한다.

• 직관적으로 생각하면, 신경망의 초기 층에서 모서리와 같은 간단한 함수를 먼저 감지하게 하고, 그 이후의 신경망 층에서 이것들을 구성해서 더 복잡한 함수를 학습할 수 있도록 한다.

• 이 시각화는 나중에 합성곱 신경망에서 더 자세히 알아볼 수 있다

• 이 시각화의 세부 사항을 알아본다면, 초기 층에서 모서리들을 알아볼 때는 더 작은 영역을, 나중에 얼굴의 일부를 감지할 때는 더 넓은 범위를 감지해낸다는 것을 알 수 있다.

• 사진 데이터가 아닌 오디오 데이터일 때는, 첫번째 층에서는 낮은 단계의 파형을 먼저 감지함으로 소리의기본 단위를 찾는 것을 학습하여, 다중에는 단어와 문장들을 인식하게 할 수 있다.

💡 측 신경망의 초기 층들은 간단한 함수를 계산하며, 이후 층에서 초기 층에서 계산한 값들을 모아 더 얼굴이나 단어처럼 더 복잡한 데이터를 인식할 수 있게 한다.

• 신경과학자들은 이 과정이 인간의 뇌가 사물을 인식하는 과정과 비슷하다고도 한다.
  • 이렇게 비유하는 것을 조심할 필요가 있긴 하지만, 완전히 틀린 것은 아니기 때문에 신경망을 더 쉽게 이해하기 위해 이 비유를 사용하는 것은 나쁘지 않다

회로 이론과 딥러닝 Circuit Theory and DL

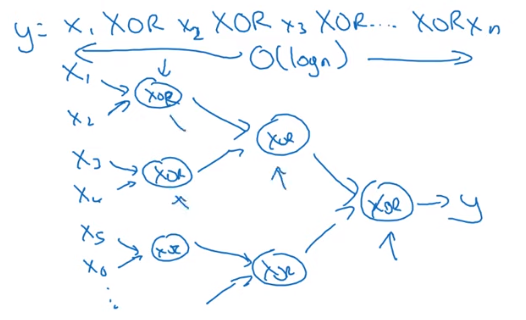
Informally : There are functions you can compute with a “small” L-layer deep neural network that shallower networks require exponentially more hidden units to compute.

• 회로 이론에서 같은 계산을 할 때, 상대적으로 얕은 신경망으로 활용하면, 깊은 신경망으로 계산할 때보다 은닉층의 개수가 기하급수적으로 증가한다.
• 이렇게 깊은 신경망을 사용하면, $O(\log n)$만에 계산을 완료할 수 있다

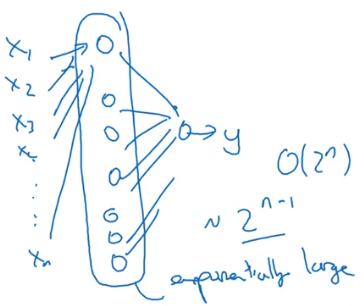
• 하지만 하나의 은닉층을 활용할 경우, 은닉층의 개수가 기하급수적으로 늘어나 $O(2^n)$만큼의 계산을 필요로하게 된다

• 그렇기 때문에, 적은 층을 활용하기보다, 더 깊은 신경망을 만들면 더 빠르게 계산할 수 있음을 회로이론을 통해 알 수 있다.

심층 신경망 네트워크 구성하기

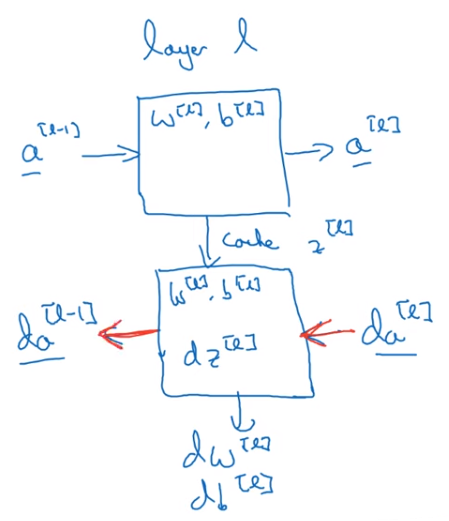
층 하나를 골라 그 층에 집중해서 계산해보자

• Layer $L$ : $W^{[l]}, b^{[l]}$
• 정방향 : 입력값 $a^{[l-1]}$, 출력값 : $a^{[l]}$
  • $z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]}$, cache $z^{[l]}$
  • $a^{[l]} = g^{[l]}(z^{[l]})$
• 역방향 : 입력값 $da^{[l]}$, 출력값 $da^{[l-1]}$, 그리고 경사하강법을 위한 $dw^{[l]}, db^{[l]}$ (cache $z^{[l]}$를 사용해서 계산)

아래 그림은 한 층의 정방향과 역방향 전파의 두 함수를 구현한 것이다

위 그림에서의 두 함수를 (두 개의 상자) 구현할 수 있다면, 전체 신경망의 계산은 다음과 같다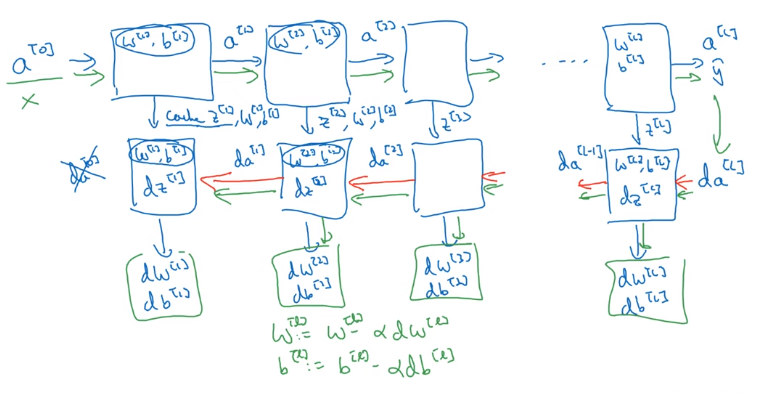

• $da^{[0]}$도 얻을 수 있지만, 입력값에 대한 도함수이기 때문에 신경망의 가중치를 학습하는 데 아무런 의미가 없기 때문에 굳이 계산하지 않아도 괜찮다.
• 박스 안에 있는 값들은 각 박스에서의 결과값을 내기 위해 사용된 변수들이다
• 각 박스에서 계산된 $dw^{[l]}$값들로 각 $W^{[l]}$와, $db^{[l]}$로 $b^{[l]}$를 계산한다.
• 여기에서 cache $z^{[l]}$는 역방향 전파를 위해 저장하는 값일 뿐만 아니라, $W^{[l]}$값과 $b^{[l]}$값도 값이 저장하여, 이 값들을 얻어 역방향 전파에 넣기 위해 사용된다.
• 그리고 이 $dw^{[l]}, db^{[l]}$값들을 통해 $W^{[l]}, b^{[l]}$를 업데이트한다.

정방향 전파와 역방향 전파

정방향 전파

정방향 전파의 입력값 : $a^{[l-1]}$

정방향 전파의 결과값 : $a^{[l]}$, 그리고 cache $z^{[l]},$ 즉 $w^{[l]}, b^{[l]}$도 포함된 값

• $z^{[l]} = W^{[l]} a^{[l-1]} + b^{[l]}$
• $a^{[l]} = g^{[l]}(z^{[l]})$, where $g$ is the activation function

위 식을 벡터화한다면,

• $Z^{[l]} = W^{[l]}A^{[l-1]} + b^{[l]}$
• $A^{[l]} = g^{[l]}(Z^{[l]})$

역방향 전파

역방향 전파의 입력값 : $da^{[l]}$

역방향 전파의 결과값 : $da^{[l-1]}$와 업데이트를 위한 $dW^{[l]}, db^{[l]}$

여기서 $dW^{[l]}, db^{[l]}$를 계산하기 위해 정방향 전파에서 캐시로 저장해뒀던 $z^{[l]}, w^{[l]}, b^{[l]}$를 사용한다.

• $dz^{[l]} = da^{[l]} \times g^{[l]\prime} (z^{[l]})$
  • 마지막 줄의 $da^{[l-1]} = W^{[l]T}dz^{[l]}$를 적용한다면 이 식이 나온다
  • $dz^{[l]} = W^{[l+1]T}dz^{[l+1]} \times g^{[l]\prime}(z^{[l]})$
  • 또한 이 식은 요소별 곱셈이기 때문에 이 4개의 식만 있으면 충분하다
• $dW^{[l]} = dz^{[l]} a^{[l-1]}$
• $db^{[l]} = dz^{[l]}$
• $da^{[l-1]} = W^{[l]T} dz^{[l]}$

위 식을 벡터화하면,

• $dZ^{[l]} = dA^{[l]} \times g^{[l]\prime}(Z^{[l]})$
• $dW^{[l]} = \frac{1}{m} dZ^{[l]} A^{[l-1]T}$
• $db^{[l]} = \frac{1}{m}$ np.sum $(dZ^{[l]}$, axis=1, keepdims=True)
• $dA^{[l-1]} = W^{[l]T} dZ^{[l]}$

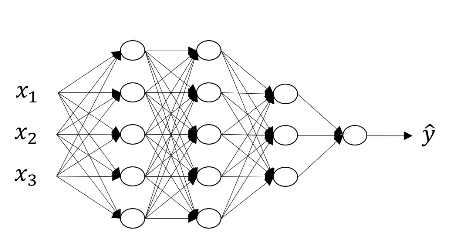
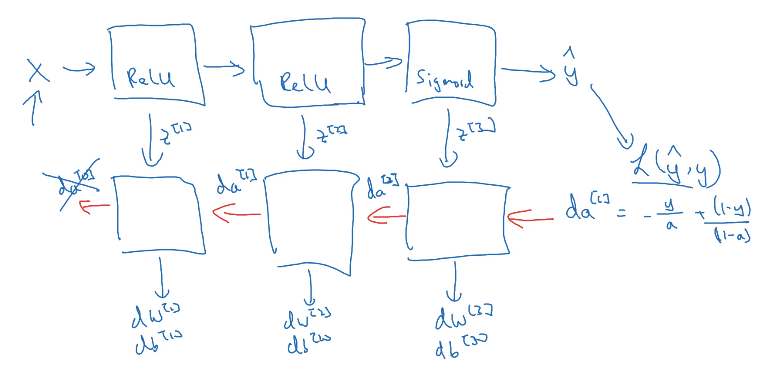
아래 그림은 2개의 은닉층과 하나의 출력층을 가진 신경망의 모습이다

• 정방향 전파는 입력 데이터 $X$로 초기화한다.
• 정방향 전파에서 $\hat{y}$를 결과값으로 가져 비용함수를 계산한 후, 역방향 전파를 한다.
• 역방향 전파는 $da^{[l]} = -\frac{y}{a}+ \frac{(1-y)}{(1-a)}$ 로 초기화한다.
  • y의 예측값, 즉 a에 대해 손실함수 L을 미분하면 이 값을 구할 수 있다.
  • 위 식을 벡터화하면 $dA^{[l]} = (\frac{y^{(1)}}{a^{(1)}} + \frac{(a-y^{(1)})}{(1-a^{(1)})}\dots -\frac{y^{(m)}}{a^{(m)}} + \frac{(a-y^{(m)})}{(1-a^{(m)})})$

변수 vs 하이퍼파라미터

효과적으로 신경망을 학습시키기 위해서는 매개변수들 뿐만 아니라 하이퍼파라미터들도 잘 업데이트 시켜야한다.

• parameters : $W^{[1]}, b^{[1]}, W^{[2]}, b^{[2]}, \dots$
• hyperparameters : learning rate $\alpha$, number of iterations, number of hidden layers $L$, number of hidden units $n^{[1]}, n^{[2]}, \dots$, choice of activation function

💡 Hyperparameter : $W$와 $b$를 통제하는 값들, 즉 최종 매개변수(파라미터)들의 최종 값을 결정하는 변수들이다.

• 하이퍼 파라미터가 많이 없던 딥러닝 초기에는 $\alpha$값이 자주 파라미터라고 불리곤 했는데, 이제는 잘 구분 지을 필요가 있다.

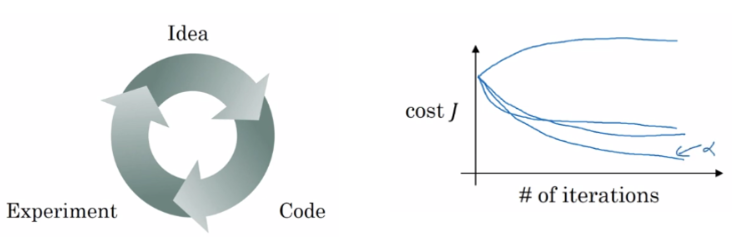
딥러닝은 경험적인 과정 (empirical process)

• 경험적인 과정이라는 것은 많은 것을 시도하고 작동되는지를 확인하고 수정하는 과정이다.
• 만약 $\alpha=0.01$로 가정하고 (idea) 코드를 짜서 (code) 학습을 (experiment) 한다고 해보자. 결과에 따라 이 $\alpha$값을 $0.01$으로 바꿀 수 있다. 옆에 cost-iteration 그래프처럼 하이퍼파라미터들을 변경해가면서 성능을 확인해보고, 그중 가장 좋은 성능을 내는 값을 선택할 수 있다.

• 딥러닝은 많은 분야에서 오디오, 이미지, 텍스트 데이터와 같은 다양한 종류의 데이터를 다루고 있다. 그리고 이 다양한 데이터마다 하이퍼파라미터에 대한 직관은 다르기 때문에, 매번 할 때마다 다양한 시도를 해야한다.
• 그렇기 때문에 새로 시작하는 사람들은 다양한 범위의 값을 시도해보고 범위를 좁혀가는 것을 조언한다.
• 또한 CPU, GPU, 네트워크, 데이터 등 다양한 조건들이 있고 이 것들도 항상 변화하고 있기 때문에, 항상 다양한 하이퍼파라미터들을 확인해보는 과정이 필요하다.

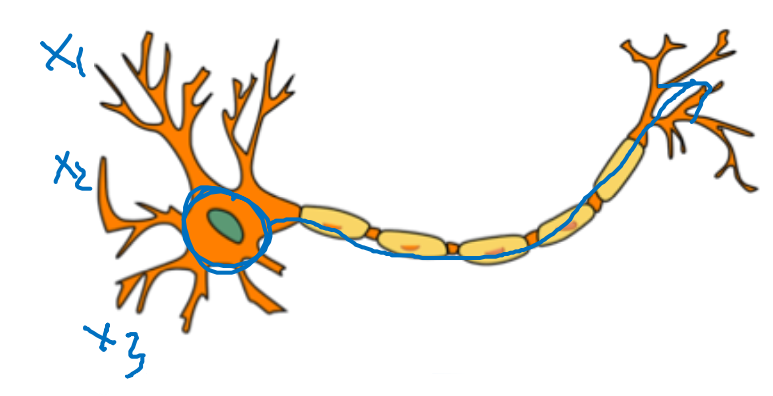
인간의 뇌와 어떤 연관이 있을까

• 뇌의 신경 세포인 뉴런은 다른 유런으로부터 전기적 신호를 받아 계산을 하고 다른 뉴런으로 전기 신호를 보낸다.
• 이렇게 간단한 로지스틱 유닛과의 비유를 들 수 있다.
• 하지만 현재 인간의 이해력으로는 인간의 뇌의 뉴련이 어떤 방법으로 정보를 계산하는지 알 수 없고, 또한 인간의 뇌가 경사 하강법과 같은 알고리즘을 활용하는지도 불분명하다.
• 인간의 뇌가 활용하는 학습 원리는 신경망의 것과 완전히 다를 수도 있다.
• 초반에는 딥러닝이 인간의 뇌에서 영감을 받아 시작만, 갈 수록 딥러닝과 뇌의 비유는 무너지고 있다.