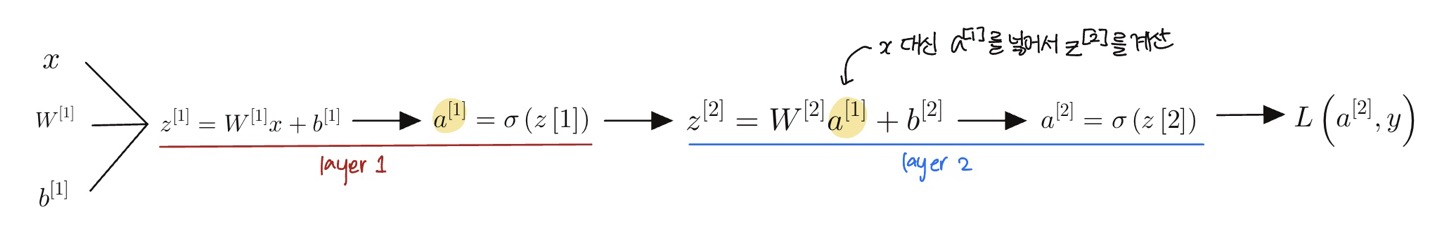03 얕은 신경망 네트워크

boostcourse의 [딥러닝 1단계: 신경망과 딥러닝] 강의를 수강 후 요약한 내용

개요

• 로지스틱 회귀에서는 (1) 특정 관측치 $x$, 그리고 매개 변수 $w$랑 $b$를 이용해서 $z$를 계산하고, (2) 이 $z$값을 활성함수에 넣어 $a$를 구한 후, (3) 손실함수를 구할 수 있다.
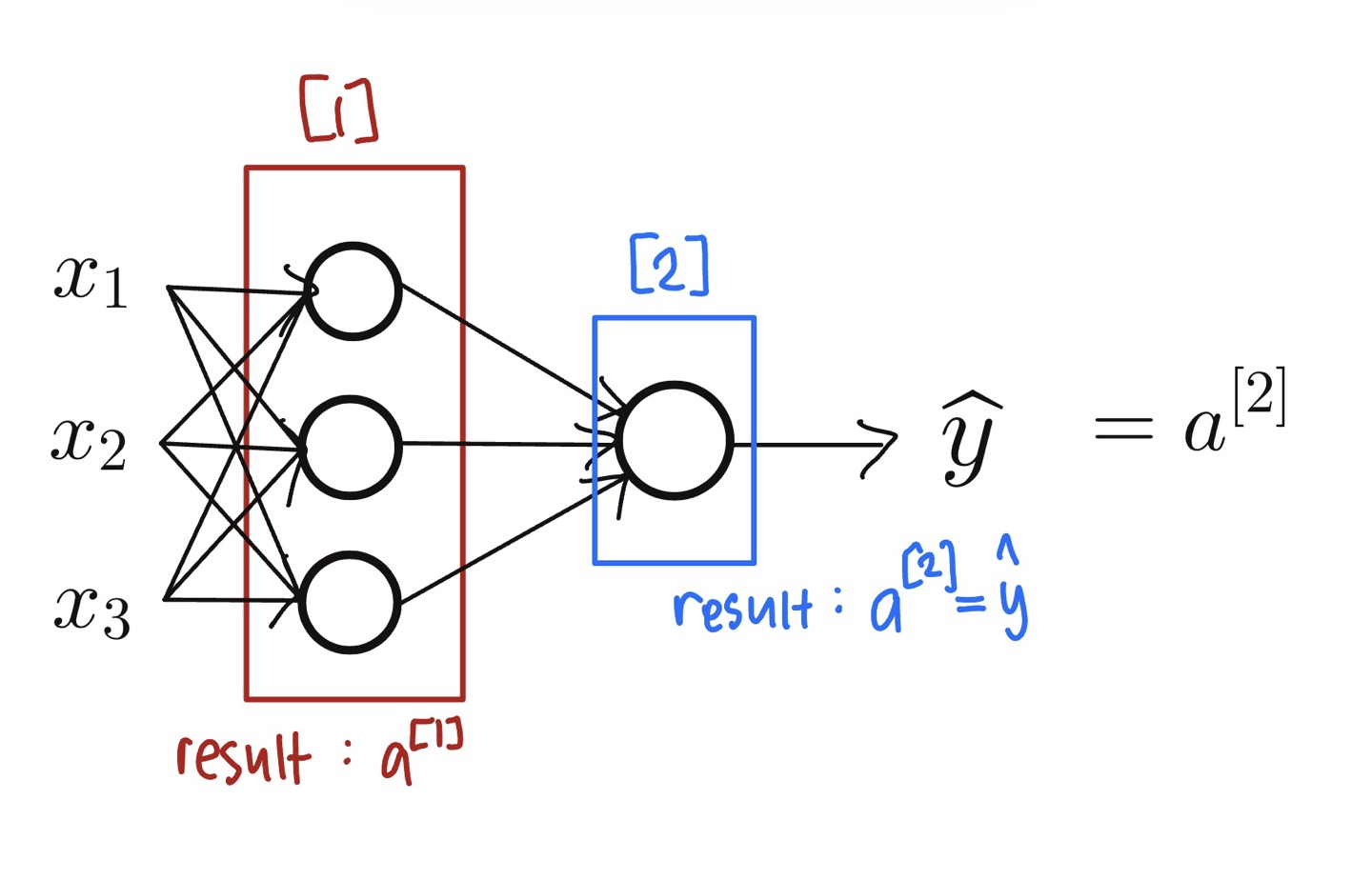
• 신경망은 여러개의 로지스틱 회귀를 쌓은 것을 의미한다. 관측치 $x$와 변수 $w^{[1]}$랑 $b^{[1]}$를 이용해서 $z^{[1]}$를 구한다. 이후 로지스틱 회귀랑 똑같이 활성함수에 넣어 $a^{[1]}$를 구한다.
• 구한 $a^{[1]}$를 $z^{[2]}$를 만드는 데 사용한다. 여기서 $x$값 대신 $a^{[1]}$를 넣어서 만드는 것. 이후 똑같이 활성함수에 넣어 $a^{[2]}$를 만들어주고 이 $a^{[2]}$로 손실함수를 계산한다.

신경망 네트워크의 구성

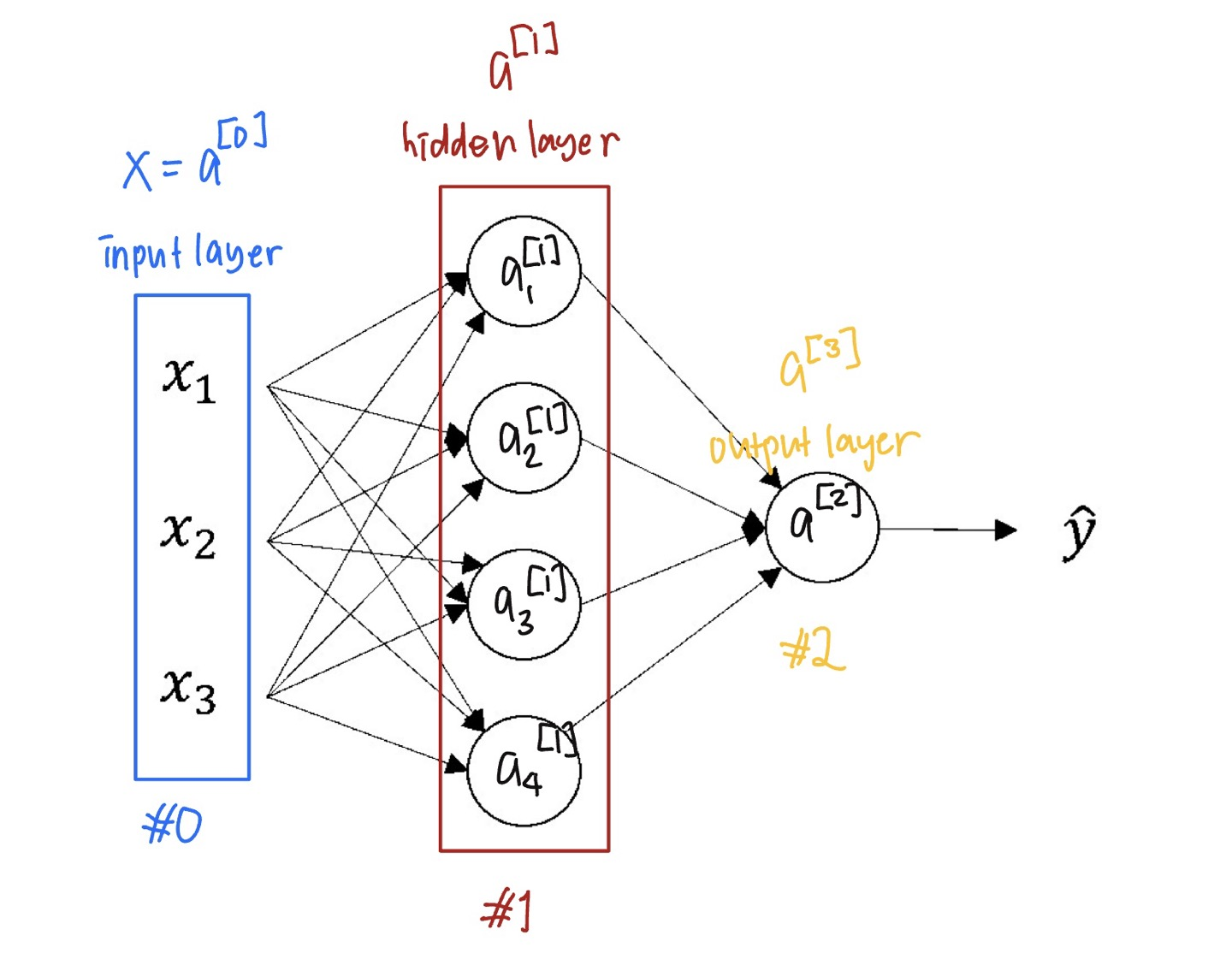
1. 입력층 Input Layer $(x)$
2. 은닉층 Hidden Layer
3. 출력층 Output Later $(y)$

• 은닉층인 ‘은닉’인 이유는, 은닉층의 실제 값들을 입력값 $x$와 출력값 $y$로 이루어진 훈련 세트에서 볼 수 없기 때문에 은닉층이라고 부른다.
• 전엔 입력층의 벡터를 $X$로 표현했는데, $a^{[0]}$로 표현할 수 있다.
• $a^{[1]}$는 $(4, 1)$의 벡터이다.
• 은닉층은 매개 변수 $w^{[1]}$와 $b^{[1]}$과 연관되어있고, 출력층은 $w^{[2]}$와 $b^{[2]}$과 연관이 되어있다.
• 관례적으로 입력층은 신경망 네트워크의 층을 셀 때 포함시키지 않는다. 그렇기 때문에 이 예제는 2층 신경망이라고 할 수 있다.

신경망 네트워크 출력의 계산

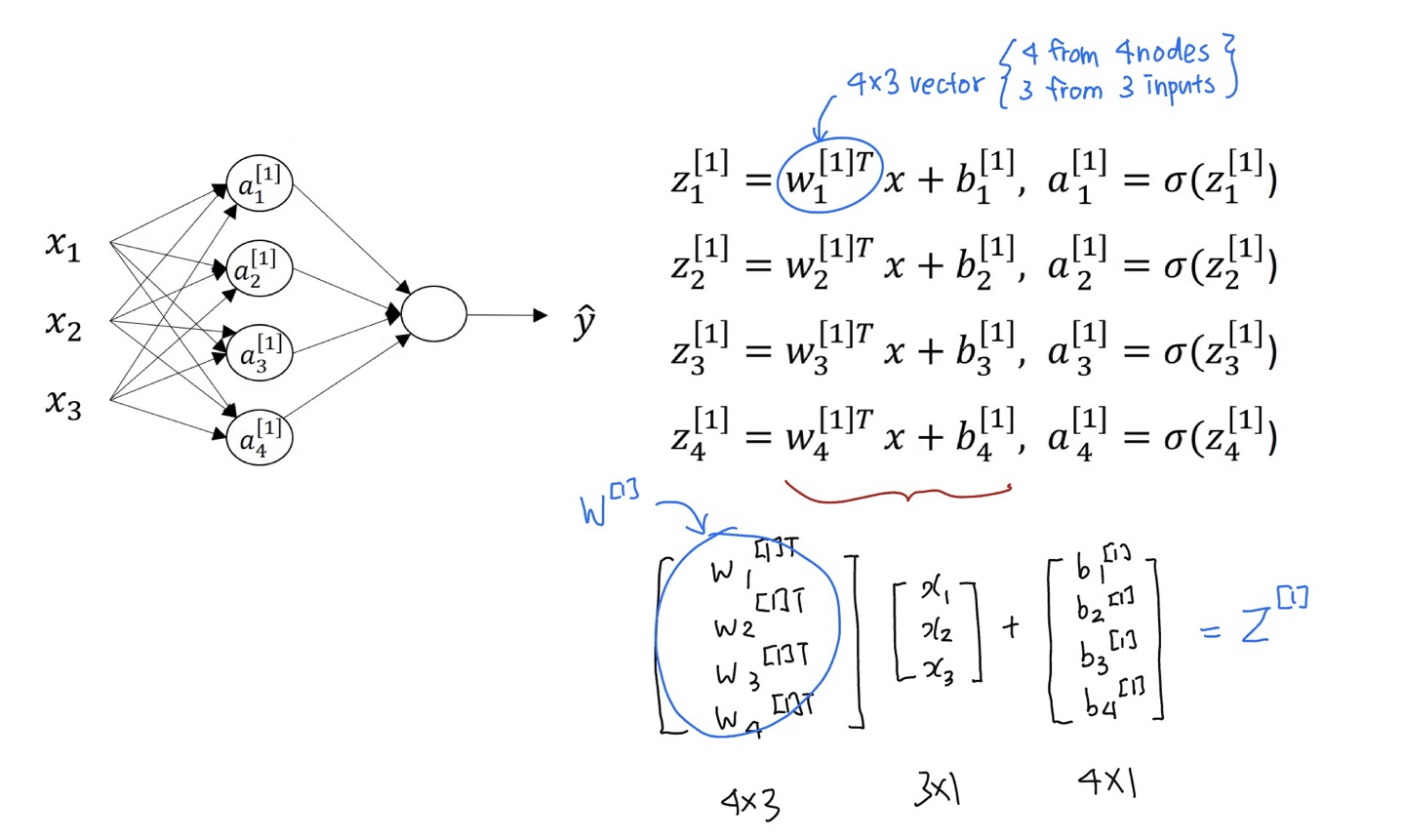
• 로지스틱 회귀의 한 원(=노드)는 두 단계의 계산을 나타낸다
  • $z=w^Tx+b$
  • $a=\sigma(z)$
• $w_1^{[1]T}$는 $(4,3)$ 벡터이며, 4개의 노드들이 있기 때문에 4개의 열을 갖고 있고, 3개의 입력 특성이 세 개이기 때문에 3개의 행을 갖고 있다.

$a_i^{[l]}$ 표기법

• $l$ : 몇 번째 층인지
• $i$ : 해당 층에서 몇 번째 노드인지

• for문을 통해 모든 계산을 하는 것이 비효율적이라는 것을 바로 알 수 있다. 벡터화를 한다면 단 4줄의 코드를 통해 이 모든 계산을 할 수 있다.

• $z^{[1]} = W^{[1]}\(x\)+b^{[1]}$ $\longrightarrow$ $z^{[1]} = W^{[1]}\(a^{[0]}\)+b^{[1]}$
• $a^{[1]} = \sigma(z^{[1]})$
• $z^{[2]} = W^{[2]}a^{[1]}+b^{[2]}$
• $a^{[2]} = \sigma(z^{[2]})$

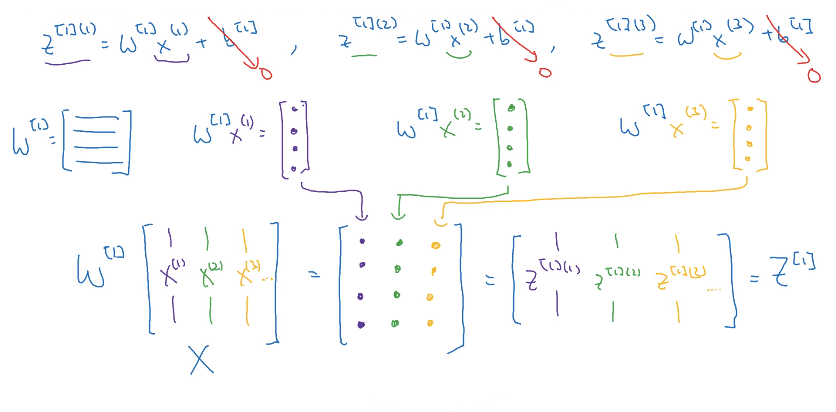
많은 샘플에 대한 벡터

• $m$개의 $x$가 있을 때, 위 4개의 코드를 $m$번 반복해야한다.

for i=1 to m: $z^{[1] (i)} = W^{[1]}\(x^{(i)}\)+b^{[1]}$
$a^{[1] (i)} = \sigma(z^{[1] (i)})$ $z^{[2] (i)} = W^{[2]}a^{[1] (i)}+b^{[2]}$ $a^{[2] (i)} = \sigma(z^{[2] (i)})$

• 그렇게 $[\space]$ 안에 있는 값은 노드의 개수이고, $(\space)$ 안에 있는 값은 $x$의 개수가 된다
• 여기서 각 $x$는 훈련 샘플을 열로 쌓은 $(n_x, m)$ 배열임을 기억해야한다.
• $x$를 $(n_x, m)$ 배열로 만들었던 것처럼, $z^{[1] (i)}$들과 $a^{[1] (i)}$들도 배열로 만들어서 벡터화 시켜줄 것이다.

\[Z^{[1]} = \begin{bmatrix} \\ z^{[1](1)} & z^{[1](2)} & ... & z^{[1](m)} \\ {} \end{bmatrix}\] \[A^{[1]} = \begin{bmatrix} \\ a^{[1](1)} & a^{[1](2)} & ... & a^{[1](m)} \\ {} \end{bmatrix}\]

• 여기서 열의 개수는 은닉층의 노드의 개수이고, 행의 개수는 $m$개의 훈련 샘플의 개수이다 (가로 안의 값).
• 그렇게 위 코드처럼 for문을 쓰는 대신, 벡터화를 통해 아 4개의 코드로 대체한다.
  • $Z^{[1]} = W^{[1]}X+b^{[1]}$
  • $A^{[1]} = \sigma(Z^{[1]})$
  • $Z^{[2]} = W^{[2]}A^{[1]}+b^{[2]}$
  • $A^{[2]} = \sigma(Z^{[2]})$

벡터화 구현에 대한 설명

• 설명을 더 간단히 하기 위해서 $b^{[1]}$를 생략한다. 어차피 상수를 모든 값에 더해주는 것이기 때문에 큰 문제가 없을 것
• $W^{[1]}$을 열벡터 $x^{(i)}$에 곱해주면 각각 열벡터가 나올 것이다.
• 결과가 열벡터이기 때문에 만약에 각 열벡터 $x^{(i)}$들을 하나의 벡터로 합친 배열 $X$를 $W^{[1]}$와 곱해줘도 하나의 배열 $Z^{[1]}$로 문제없이 나올 수 있는 것이다.
• 즉, 입력값을 열로 쌓는다면, 결과도 열의 형식으로 나온다.

활성화 함수

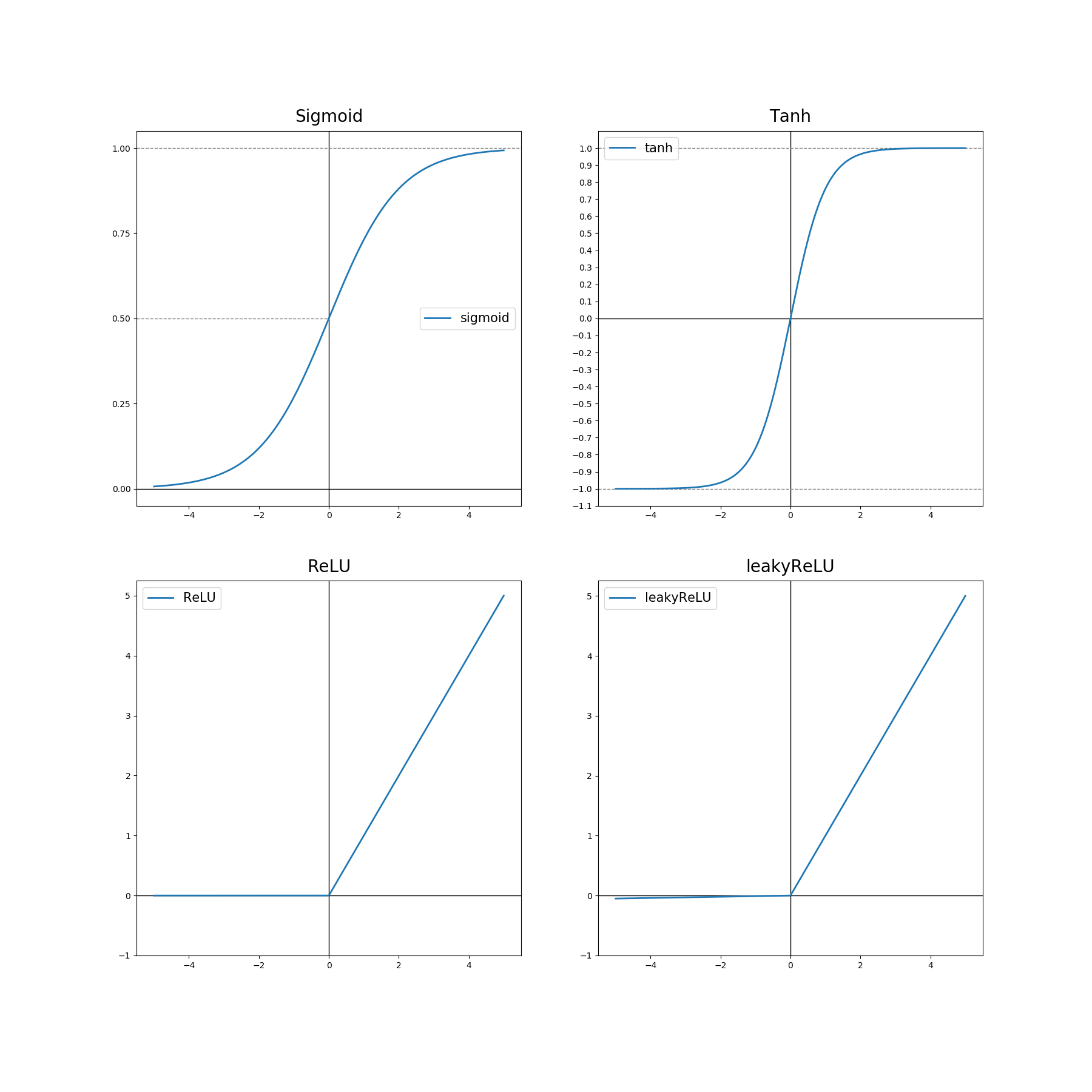
신경망을 만들 때, 은닉층과 출력층에서 어떤 활성화 함수를 사용해야하는지 선택해야한다.

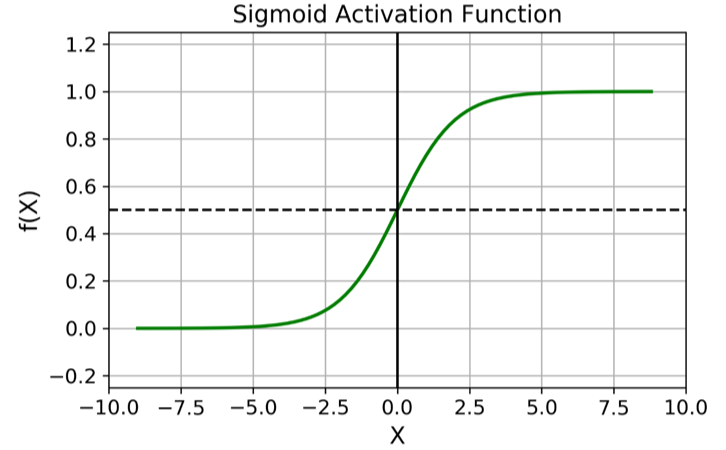
• sigmoid function : $a=\frac{1}{1+e^{-z}}, 0<a<1$
  • sigmoid는 결과값이 0과 1 사이에서 나오기 때문에 대부분 이진 분류의 출력층(마지막 층)에서 사용한다.
• tanh function : $a = \tanh(z) = \frac{e^z-e^{-z}}{e^z-e^{-z}}, -1<a<1$
  • 수학적으로 sigmoid를 옮긴 것. sigmoid와 비슷하지만 원점을 지나고 비율이 다르다.
  • 이 함수는 평균값이 0에 가깝기 때문에 대부분의 경우 sigmoid보다 (무조건!) 성능이 좋다. 평균값이 0에 가깝기 때문에 데이터의 중심을 0.5 대신 0으로 만드는 효과를 주어 다음 층의 학습을 더 쉽게 한다.
• ReLU function (Rectified Linear Unit) : $a=\max(0,z)$
  • 활성화 함수의 기본값. 어떤 활성화 함수를 쓸지 모를 때 ReLU를 쓰면 대부분 좋은 결과를 낸다.
  • $z$가 음수일 때의 도함수가 $0$이다. 실제로는 잘 되긴 하지만, 이를 방지하기 위해 생긴 함수가 Leaky ReLU 함수이다
• Leaky ReLU : $a=\max(0.01,z)$
  • $z$가 음수일 때 도함수가 $0$이 아니라 약간의 기울기를 준다.
  • ReLU보다 좋은 결과를 주지만, 실제로는 많이 사용하지 않는다.
  • ReLU와 Leaky ReLU 모두 대부분의 $z$에 대해 활성화 함수의 기울기가 0이 아니기 때문에 신경망이 훨씬 더 빠르게 학습할 수 있다.
  • 여기서 나오는 0.01는 임의로 변경할 수 있는

💡 활성화 함수의 기울기가 0에 가까워지면 (즉, 함수가 직선의 형태에 가까워지면) 학습 속도가 느려진다. 그렇기 때문에 sigmoid의 학습 속도가 $z$값이 커지면 커질수록 더 느려지기 때문에 성능이 좋지 않음을 알 수 있다.

비선형 활성화 함수를 쓰는 이유

• 만약 비선형 활성화 함수를 쓰지 않으면 이 모델은 $\hat{y}$를 입력 특성인 $x$에 대한 선형 함수로 내보낸다.
  • 즉 $a^{[1]} = z^{[1]} = W^{[1]}x + b^{[1]}$, $y= ax+b$의 형태의 함수를 내보내는 것
  • 또는 은닉층이 없는 것과 다르지 않다
• 그렇기 때문에 만약 비선형 활성화 함수를 쓰지 않는다면, 선형 함수 그 이상의 차이를 줄 수 없다. 아무리 신경망이 깊어져도 흥미로운 계산을 할 수 없다.
• 하지만 회귀 문제에 대한 머신러닝을 할 때에는 출력층에서 비선형 활성화 함수를 사용한다.
  • 만약 $y$가 실수값이라면 사용할 수 있다는 것.
  • 아무리 회귀 문제여도 은닉층에서는 ReLu와 같은 비선형 활성화 함수를 사용해야한다.

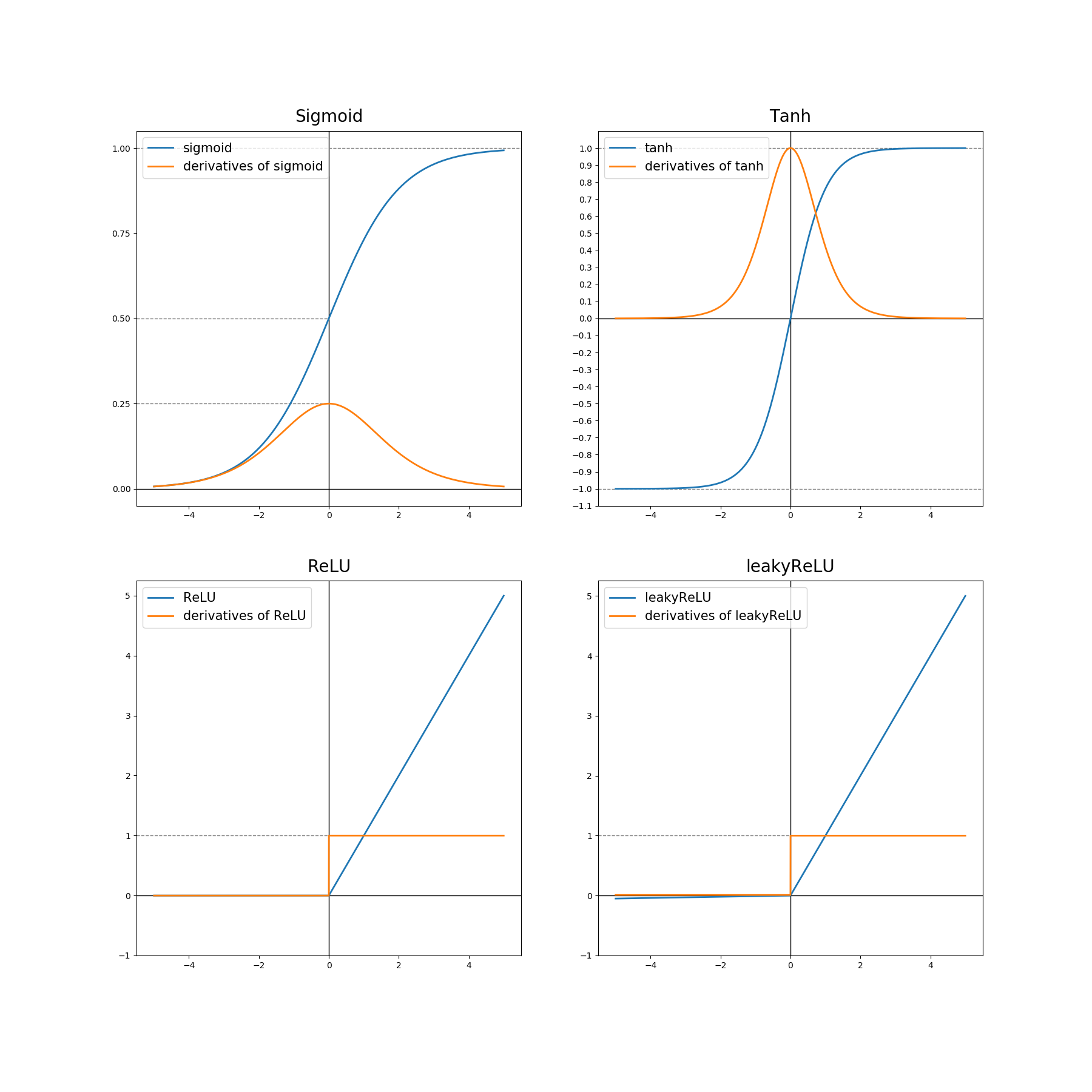
활성화 함수의 미분

• 시그모이드 활성화 함수 $g(z)=\frac{1}{1+e^{-z}}$의 미분값은

\[g\prime(z)=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}}) = g(z)(1-g(z))\]

• Tanh 활성화 함수 $g(z)=\tanh (z)$의 미분값은

\[g\prime(z)=1-(\tanh(z))^2\]

• ReLU 활성화 함수 $g(z) = \max(0,z)$의 미분값은

\[g\prime(x) = \begin{cases} 0 & z<0 \\ 1 & z \ge 0 \end{cases}\]

• Leaky ReLU 활성화 함수 $g(z) = \max(0.01z,z)$의 미분값은

\[g\prime(x) = \begin{cases} 0.01 & z<0 \\ 1 & z \ge 0 \end{cases}\]

신경망 네트워크와 경사 하강법

한 층의 은닉층을 가진 신경망의 경사 하강법에 대한 설명

• 매개 변수 $w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}$를 갖고 있다.
• 만약 $n_x$가 있다면, 이 $n_x$는 $n^{[0]}, n^{[1]}, n^{[2]}$로 이루어져있다.
  • 입력층의 개수 : $n^{[0]}$
  • 은닉층의 개수 : $n^{[1]}$
  • 출력층의 개수 : $n^{[2]}$
• 그렇기 때문에 각 매개 변수의 배열의 차원은 다음과 같다:
  • $w^{[1]}$ : $(n^{[1]}, n^{[0]})$
  • $b^{[1]}$ : $(n^{[1]}, 1)$
  • $w^{[2]}$ : $(n^{[1]}, n^{[1]})$
  • $b^{[2]}$ : $(n^{[1]}, 1)$
• 이진 분류를 하고 있다고 가정하면, 비용함수는 $J(w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}) = \frac{1}{m}\sum^n_{i=1}L(\hat{y}=a^{[2]}, y)$

알고리즘에서 이 변수들을 훈련시키기 위해서 경사하강법을 사용해야한다. 신경망을 훈련시킬 때는 $w$값을 0이 아닌 랜덤한 값으로 초기화하는 것이 중요하다.

1. 변수를 초기화 시킨 후, 경사하강법을 실행할 때마다 예측값($= \hat{y}^{(i)}, i=1, \dots, m$)을 계산한다
2. $w$에 대한 도함수와 $b$에 대한 도함수를 계산한다.
   • $dw^{[1]} = \frac{dJ}{dw^{[1]}}$
   • $db^{[1]} = \frac{dJ}{db^{[1]}}$
3. $w$를 업데이트 시킨다.
   • $w^{[1]} \coloneqq w^{[1]} - \alpha \space dw^{[1]}$, where $\alpha$ is the learning rate
   • $b^{[1]} \coloneqq b^{[1]} - \alpha \space db^{[1]}$

여기서 중요한 것은 이 편미분(= backward propagation)들을 어떻게 계산하는지다.

💡 순전파와 역전파 한 줄 복습 (출처)

• 순전파 : 모델의 입력층부터 출력층까지 순서대로 변수들을 계산하고 저장하는 것
• 역전파 : 매개 변수들에 대한 도함수, 즉 기울기를 계산하는 과정

경사하강법 : 순전파

• $Z^{[1]} = w^{[1]}X + b^{[1]}$
• $A^{[1]} = g^{[1]}(Z^{[1]})$
• $Z^{[2]} = w^{[2]}A^{[1]} + b^{[2]}$
• $A^{[2]} = g^{[2]}(Z^{[2]}) = \sigma(Z^{[2]})$

경사하강법 : 역전파

• $dZ^{[2]} = A^{[2]} - Y$
• $dw^{[2]} = \frac{1}{m}dZ^{[2]}A^{[1]T}$
• $db^{[2]} = \frac{1}{m}$np.sum $(dZ^{[2]},$ axis=1, keepdims = T $)$
  • 랭크1 배열을 나오지 않게 하기 위해 keepdims=T 를 사용
  • 즉 배열의 크기가 $(n^{[2]},\space)$이 아닌 $(n^{[2]}, 1)$일 수 있게 하는 것
  • keepdims=T 또는 reshape 메소드를 사용할 수 있다.
• $dZ^{[1]} = W^{[2]T}dZ^{[1]} \times g^{[1]\prime}(Z^{[1]})$
  • 여기서 $\times$는 요소별 곱셈(element-wise)이다.
  • $W^{[2]T}dZ^{[1]}$ 와 $g^{[1]\prime}(Z^{[1]})$ 모두 $(n^{[1]}, m)$ 배열이기 때문에 요소별 곱셈인 것
• $dW^{[1]} = \frac{1}{m} dZ^{[1]}X^T$
• $db^{[1]} = \frac{1}{m}$np.sum $(dZ^{[1]},$axis=1, keepdims = T$)$

역전파에 대한 이해

단일 샘플에 대한 정방향 전파(역전파)

• $dz^{[2]} = a^{[2]}-y$
• $dW^{[2]} = dz^{[2]}a^{[1]T}$
• $db^{[2]} = dz^{[2]}$
• $dz^{[1]} = W^{[2]T}dz^{[2]} \times g^{[1]\prime}(z^{[1]})$
• $dW^{[1]} = dz^{[1]}x^{T}$
• $db^{[1]}=dz^{[1]}$

벡터화

• $dZ^{[2]} = A^{[2]} - Y$
• $dW^{[2]} = \frac{1}{m}dZ^{[2]}A^{[1]T}$
  • $\frac{1}{m}$이 있는 이유 : 비용함수를 계산할 때 $m$으로 나눠줬기 때문에, 도함수를 계산할 때도 나눠준다.
• $db^{[2]} = \frac{1}{m}$np.sum $(dZ^{[2]}$, axis = 1, keepdims = True$)$
• $dZ^{[1]} = W^{[2]T}dZ^{[2]} \times g^{[1]\prime}(Z^{[1]})$
  • 위에 언급했던 것처엄 요소별 곱셈임을 기억해야한다.
  • $(n^{[1]}, m)$의 사이즈를 갖고 있는 배열!
• $dW^{[1]} = \frac{1}{m}dZ^{[1]}X^T$
• $db^{[1]} = \frac{1}{m}$ np.sum $(dZ^{[1]}$, axis=1, keepdims=True$)$

랜덤 초기화

신경망을 학습시킬 때 초기값을 랜덤하게 초기화시키는 것이 중요하다.

• 로지스틱 회귀의 경우 0으로 초기화 시키는 것이 괜찮았지만, 더 깊은 신경망에서는 0으로 초기화시켰을 경우 작동하지 않을 것
• $b$값을 0으로 초기화 시키는 것은 괜찮지만, $w$까지 0으로 초기화시키는 것은 문제가 된다.

만약 $w$값이 0이라면, 모든 은닉층이 같은 함수를 계산하고 있을 것(=은닉층의 유닛이 대칭)이다. 즉, 모든 은닉층의 유닛이 출력층에 같은 영향을 미치게 될 것이다. 그렇게 된다면, 이 신경망을 한번 더 학습해도, 같은 결과를 나타내게 될 것이다.

더 큰 신경망을 갖고 있더라도, 만약 초기값이 0이라면, 모든 은닉층이 대칭이 될 것이고, 경사하강법을 몇번을 돌리더라도 모든 유닛은 항상 같은 함수를 계산하게 될 것이다.

그래서 이것을 해결하기 위해 변수를 랜덤하게 초기화시킨다.

w[1] = np.random.rand((2,2)) * 0.01   #Create an array of the given shape and populate it with random samples from a uniform distribution over [0, 1).

b[1] = np.zero((2,1))  #위에 언급되었듯, b는 초기값을 0으로 설정해도 은닉층의 유닛들이 대칭이 되는 문제를 일으키지 않는다.

그렇다면 왜 0.01 로 곱해주는 것일까?

왜냐하면 가중치의 초기값을 매우 작은 수로 설정해주는 것이 좋기 때문이다

예를 들어 sigmoid 함수를 활성 함수로 사용한다고 해보자.

• $z^{[1]} = w^{[1]}x+b^{[1]}$
• $a^{[1]} = g^{[1]}(z^{[1]})$

$w$값이 크다면, $z$값도 매우 큰 값이나 작은 값이 나올 것이다. 이 값이 sigmoid 함수에 들어간다면 학습에 초기부터 $z$값이 활성화 함수의 두꺼운 부분, 즉 기울기가 0으로 수렴하는 부분의 값이 나오게 될 것이다. 위 부분에서 나왔듯이, 만약 기울기가 0으로 수렴한다면 학습속도가 느려지기 때문에 문제가 발생하는 것이다.

하지만 어쩔 때는 0.01보다 더 좋은 수가 있을 수도 있다

• 만약 한 개의 은닉층을 가직 얕은 신경망을 학습시킨다면, 이 숫자도 좋은 값일 것이다.
• 하지만 더 깊은 신경망을 학습할할 때는 이보다 더 좋은 값이 있을 수 있다.

💡 여기서 가장 중요한 것은, 기울기가 0으로 수렴하지 않게 하기 위해서 $w$ 의 초기값을 작고 랜덤한 값으로 설정해주는 것.