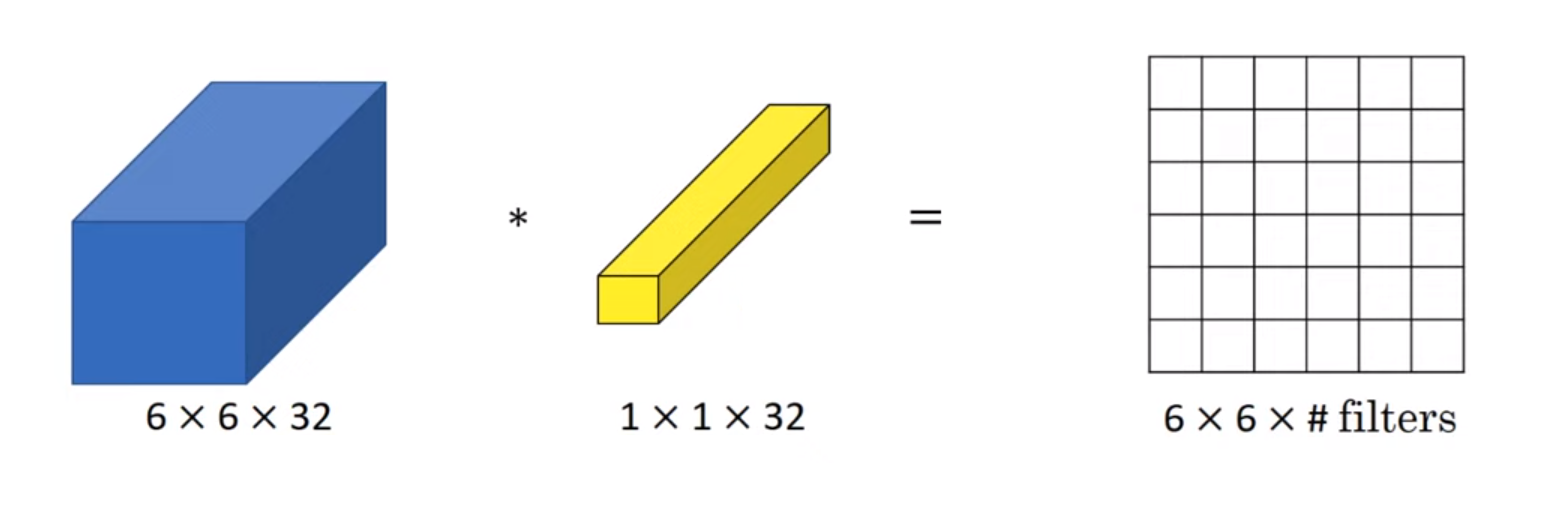13 고전적인 네트워크들

왜 케이스 스터디를 하나요?

사례들을 살펴보는 이유

• 합성곱 층, 풀링 층, 완전 연결 층과 같은 합성곱 신경망의 기본 구성 요소들의 효과적인 조합에 대한 intuition을 얻기 위해
• 한 컴퓨터 비전 작업에서 잘 작동하는 경우는 다른 작업에서도 대체적으로 잘 작동하는 경우가 많다.

고전적인 네트워크들

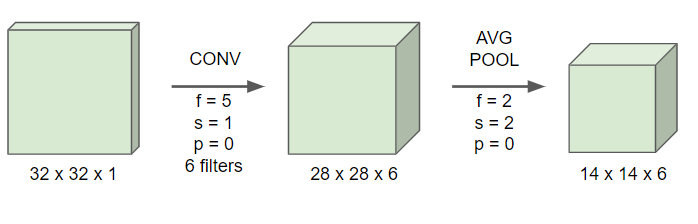
LeNet-5

목적 : 흑백 손글씨 숫자 인식

16주차의 마지막 예시와 비슷하다

• 6개의 필터를 사용하기 때문에 차원이 늘어나고, 패딩을 사용하지 않기 때문에 이미지 사이즈가 감소한다.
• 당시에는 최대 풀링보다는 평균 풀링을 더 많이 사용했다.
• 또 2x2 사이즈의 필터를 사용해 평균 풀링을 했기 때문에 이미지 사이즈가 또 줄어든다.

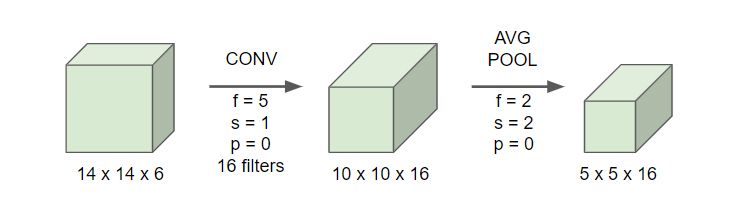
• 16개의 필터를 사용해 다시 합성곱 층을 추가해준다.
• 당시에는 패딩을 사용하지 않았기 때문에 이미지 사이즈가 줄어든다
• 풀링 층을 사용해준다.
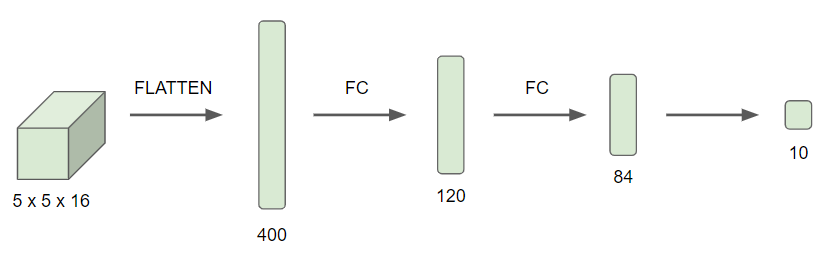
• 5x5x16 차원을 갖고 있기에 총 400개의 노드들을 갖고 있다.

• 다음에는 이 400개의 노드들을 120개의 뉴련에 각각 연결하여 완전연결 층을 만들어준다.
• 2개의 완전 연결 층을 더 해주어 10개의 class를 갖는 $\hat{y}$을 예측해준다.
• 요즘이라면 소프트맥스 함수를 사용해서 분류하겠지만, LeNet-5은 현재에는 잘 사용하지 않는 방법을 사용해 분류했다.

이 신경망은 요즘 기준으로는 적은 60,000개의 파라미터들을 사용한다.

현재에는 이 신경망보다 1000배 정도 더 큰, 1000만 또는 1억개의 변수를 갖는 신경망을 사용한다.

하지만 요즘도 깊이 깊어수록 높이와 너비가 감소한다.

현재까지 이어지고 있는 패턴

1. 이미지의 차원 : 신경망이 깊어질수록 높이아 깊이가 감소하고 채널의 수가 증가한다.
2. 층들의 조합 : 1~2개의 합성곱 층 + 풀링 층이 여러개 있고, 마지막에 1~2개의 완전 연결 층이 있는 형태

또한 해당 논문에서는 요즘과는 다르게 풀링층 뒤에 비선형함수를 적용했으며, 비선형함수도 ReLU가 아닌 Sigmoid/Tanh를 사용했다.

AlexNet

• 96개의 필터를 사용하고, 필터의 스트라이드가 4이기에 이미지가 많이 축소된다 (1/4만큼).
• 풀링 층을 통과하면 더 작은 이미지가 된다.
• 같은 합성곱 층과 풀링층을 한번 더 적용해준다.

• 같은 합성곱 층을 세번 더 적용해준 후 풀링 층을 적용해준다.

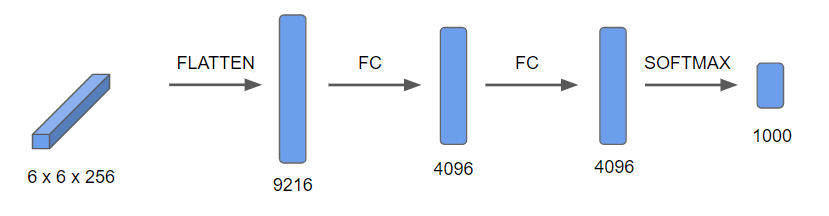
• 이 6x6x256=9216개의 노드들을 2개의 완전 연결 층에 적용시킨 후 소프트맥스를 통해 1000개의 출력 결과를 낸다.

AlexNet은 LeNet-5과 비슷한 결과를 갖지만 더 많은 파라미터들을 가진다.

• 비슷한 구성을 갖고 있어도 더 많은 은닉층들을 갖고 있기에 더 좋은 성능을 가질 수 밖에 없다.
• 또한 ReLU 활성화 함수를 사용하기 때문에 더 좋은 결과를 갖는다.

또한 논문이 쓰여질 당시 GPU의 성능이 아직 좋지 않았기 때문에 여러 GPU들을 사용해서 훈련하는 복잡한 방식을 활용했다.

이 논문을 통해 컴퓨터 비전 분야에 딥러닝이 적용될 수 있을거라는 가능성을 보여줬다.

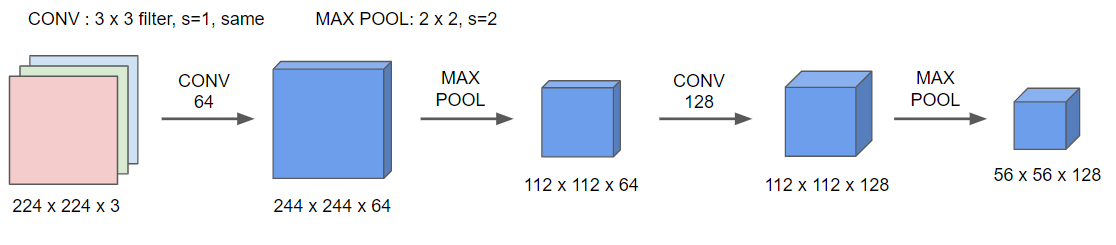
VGG

많은 하이퍼파라미터를 갖는 대신, 계속 동일한 합성곱 층의 필터와 풀링 층을 사용함으로서 간절한 구조를 갖게 했다.

• 합상곱 층 : 3x3 필터, 스트라이드 1
• 풀링 층 : 2x2, 스트라이드 2

• CONV 64 : 첫 층에서는 64개의 필터를 사용해주고, 이 합성곱을 2번 해준다. 위 그림에서는 한번만 적용된 것 같지만, 실제로는 2번의 합성곱을 하고 있다.
• 두 번의 합성곱을 한 후 풀링층을 적용해준다. 이 풀링층은 이미지 사이즈를 감소시킨다.
• CONV 128 : 필터가 128개가 있는 합성곱을 2번 해준 후 풀링 층을 적용해준다.

• CONV 256 세 번+ 풀링 층
• CONV 512 세 번+ 풀링 층
• CONV 512 세 번+ 풀링 층

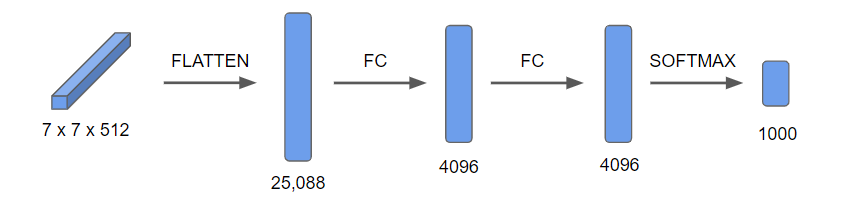
• 이 7x7x512=25088개의 노드들을 두 개의 완전 연결 층에 통과시킨 후 소프트맥스를 사용하여 1000의 클래스로 분류시킨다.

VGG-16의 16은 총 16개의 층을 갖는다는 의미이다.

이 네트워크는 총 1억 3천 8백만 개의 변수를 갖는, 현재의 기준으로서도 상당히 큰 네트워크이다.

VGG-16의 구조적인 장점 : 균일하다

• 몇 개의 합성곱 층 뒤에 풀링층으로 높이와 너비를 줄여준다.
• 또한 각 합성곱 층의 필터의 개수가 64부터 두 배씩 늘어난다.

이 구조의 상대적인 획일성이 가지는 단점은 훈련시킬 변수가 많아 네트워크의 크기가 커진다는 것이다.

하지만 깊이가 깊어질 수록 보이는 패턴 (풀링층에서 높이와 너비가 반으로 줄어들고 합성곱 층에서는 필터의 개수가 두 배가 되는 패턴)이 매우 매력적이다.

장점 : 균일한 패턴을 갖고 있다. 단점 : 훈련시킬 변수가 많다 → 네트워크가 커진다.

ResNet (Residual Network)

• 매우 깊은 네트워크들은 경사의 소실 또는 폭팔의 위험이 있기 때문에 학습시키기 어렵다.
• 이 문제를 ResNet에서 스킵 연결을 통해 해결했다.

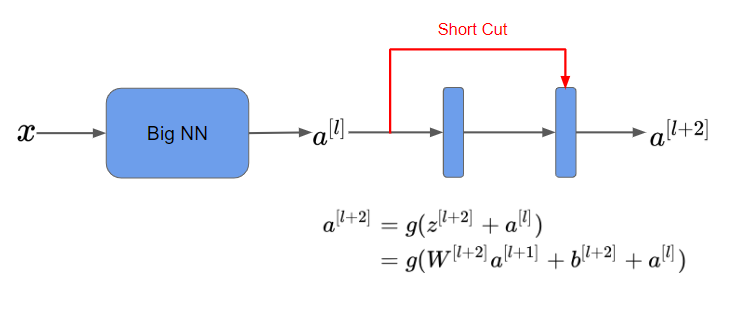
스킵 연결 : 한 층의 활성값을 가지고 훨씬 싶은 층에 적용하는 방식

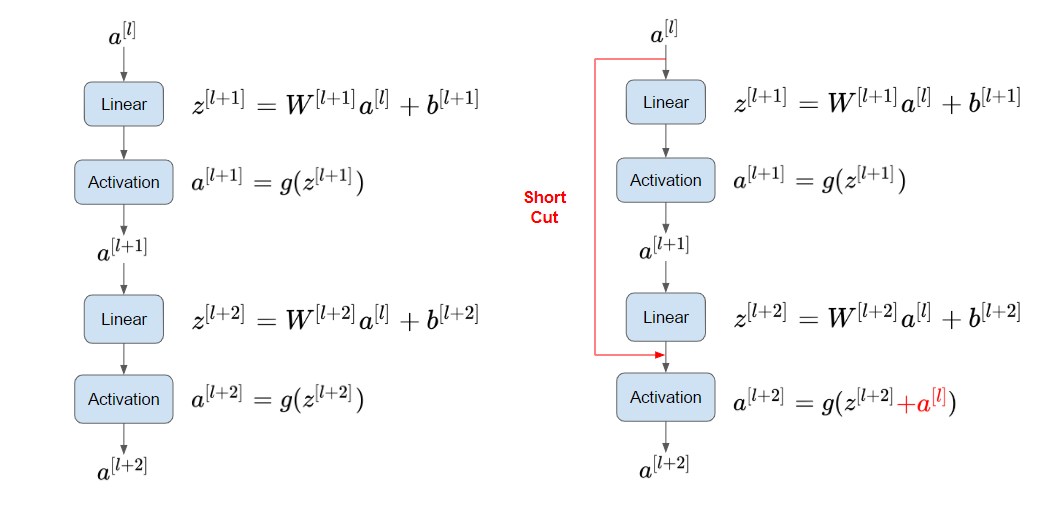
잔여 블록 Residual Block

• $a^{[l]}$을 통해 $z^{[l+1]}$를 계산한 후 ReLU 비선형성을 적용해 $a^{[l+1]}$를 계산한다.
• 다시 $z^{[l+2]}$를 계산 후 활성화 함수 ReLU를 적용해 $a^{[l+2]}$를 계산한다.

즉 $a^{[l]}$의 정보가 $a^{[l+2]}$로 흐르기 위해서는 위 과정을 거쳐야한다. 이 과정을 main path로 칭하겠다.

• ResNet에서는, $a^{[l+2]}$를 계산하기 위해, $a^{[l+1]}$를 먼저 계산하지 않고 바로 $a^{[l]}$를 사용한다.
• $a^{[l+2]}$를 구하기 위해 $z^{[l+2]}$에 활성화 함수를 바로 적용시키는 것이 아닌, 오른쪽 그림처럼 $a^{[l]}$를 더한 후 활성화 함수를 적용시키는 것이다.
• 이 $a^{[l]}$가 잔여 블록이 되는 것이다.

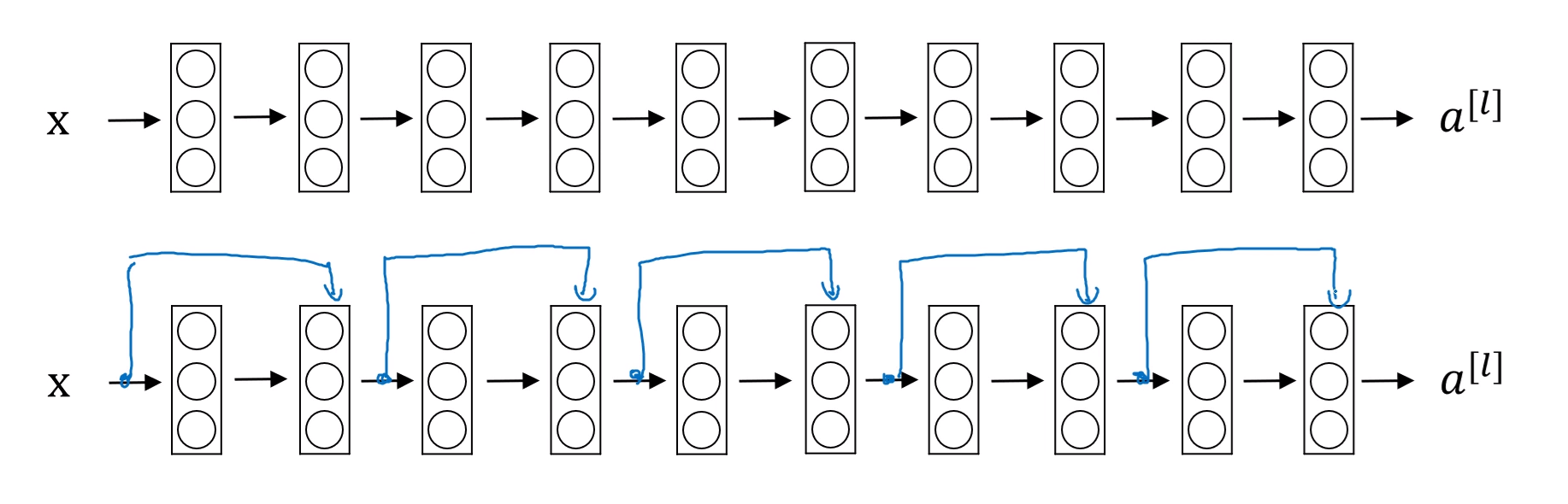
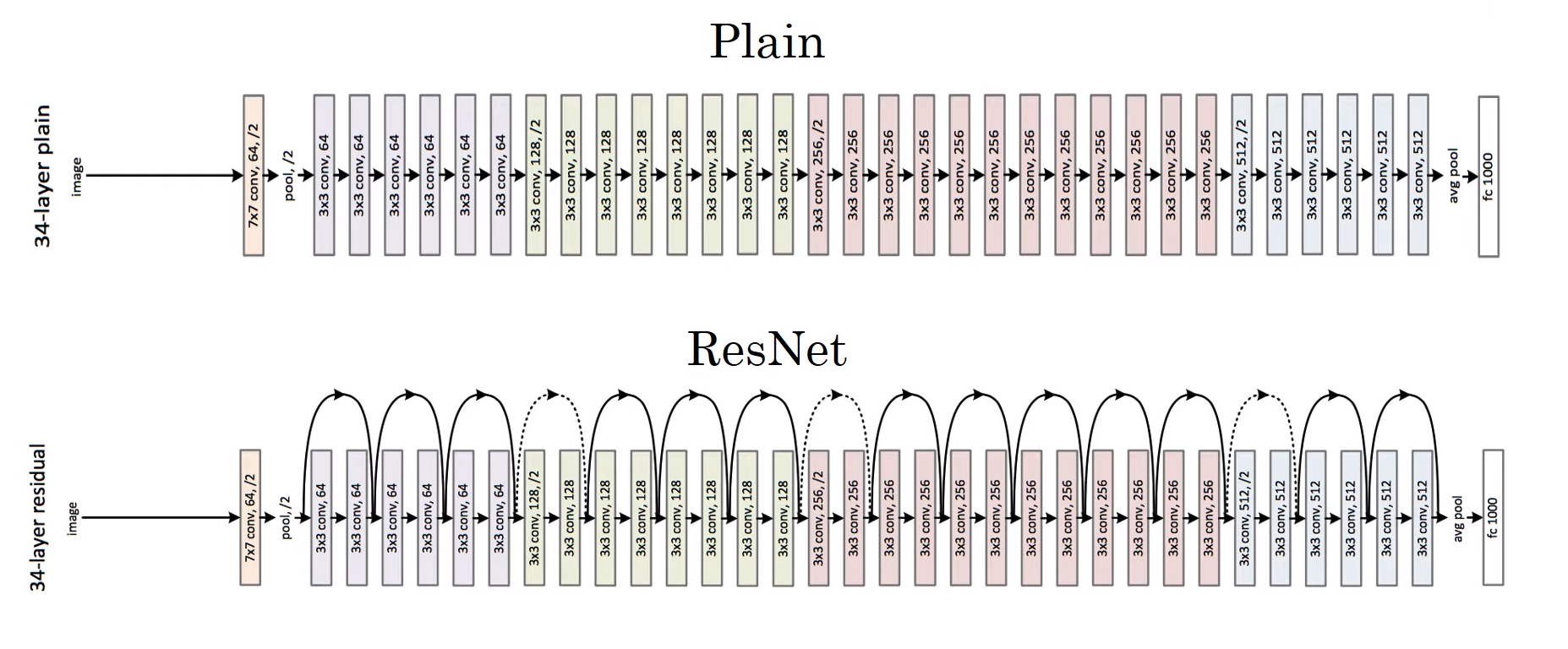
• 만약 평형망 Plain Model, 즉 잔여 블록이 없는 신경망을 ResNet으로 바꿔주기 위해서는 두 개의 층마다 스킵 연결을 더해준다.
• 이렇게 되면 총 5개의 잔여 블록이 쌓인 형태의 ResNet이 되는 것이다.

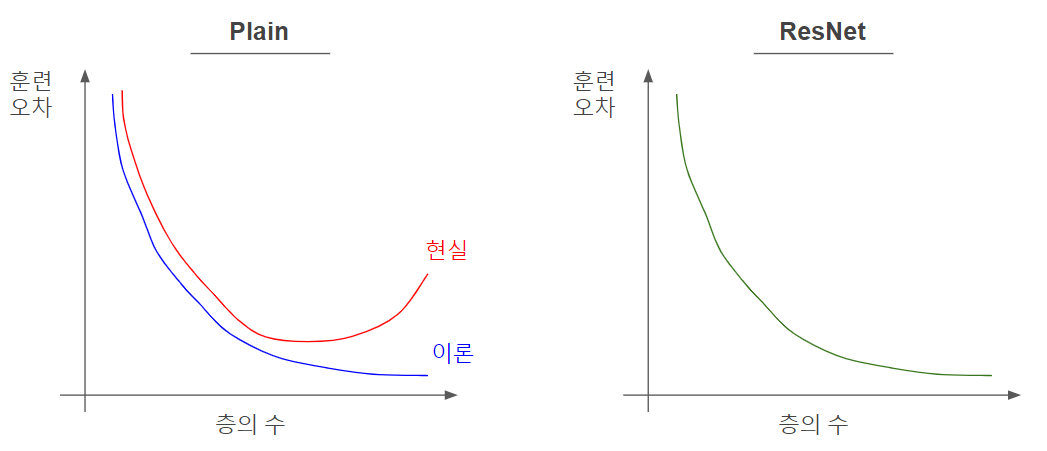
• 실제로 평형망을 학습 시킬 때의 오차는 이론상 계속 감소해야하지만, 위 그래프처럼 어느 순간부터 감소하지 않고 증가한다.
• 즉, 평형망이 깊어질수록 최적화 알고리즘으로 훈련시키기 어려워질 것이고, 오차를 줄이기 어려워진다.
• 하지만 ResNet을 사용하면, 실제로 네트워크를 학습시킬 때 아무리 층이 깊어져도 오차가 계속 줄어든다.

즉, ResNet은 스킵 연결을 사용함으로써 경사 소실 문제도 많이 해결하고, 더 깊은 신경망을 학습시킬 수 있게 하는 것이다.

왜 ResNet이 효과적일까?

왜 ResNet은 신경망의 깊이가 깊어져도 훈련세트에서의 성능이 좋을까?

• 여기서 $W^{[l+2]}$과 $b^{[l+2]}$이 $0$이라고 해본다면, $a^{[l+2]}=g(a^{[l]})$이 될 것이다.
• 또한 이 신경망에서 $g$, 즉 활성화 함수를 ReLU로 사용한다고 하면, 결국 $a^{[l+2]} = a^{[l]}$으로 항등식이 되는 것이다.
• 결국 $a^{[l+2]} = a^{[l]}$이 되기 때문에, 두 개의 층들이 더해져도 $a$값을 계산하기 훨씬 더 수월하게 되는 것이다.
• 위 이유로, 잔여 블록을 사용하게 되면 신경망의 깊이가 깊어져도 성능에 지장이 없게 되는 것이고, 또한 층이 더 깊어졌기 때문에 성능에 지장이 없는 것이 보장될 뿐만 아니라 더 좋게할 수도 있는 것이다.

$z^{[l+2]}$와 $a^{[l]}$의 차

• 또한 주의해야할 점은, $g(z^{[l+2]} + a^{[l]})$에서 $z$와 $a$가 더해지기 때문에, 이 둘의 차원이 같아야한다.
• 그렇기 때문에 ResNet에서는 아래와 같이, 3x3의 같은 합성곱 층이 여러번 반복되는 것을 볼 수 있다.

• 만약 입력값과 출력값의 차원이 다를 경우, $W_s$라는 행렬을 $a^{[l]}$에 곱해준다.
• 이 $W_s$의 차원은 결과값의 차원x입력값의 차원으로, 입력값의 차원을 결과값의 차원과 동일하게 만들어준다.

네트워크 속에 네트워크

• 만약 1차원의 행렬에 1x1 합성곱을 적용해준다면, 그냥 해당 값으로 곱해준 것과 큰 차이가 없을 것이다.
• 하지만 2차원 이상의, 즉 아래 예시를 본다면 6x6x32 차원을 갖는 행렬에 1x1x32 합성곱을 해주고 ReLU 비선형성을 더해준다면, 해당 줄에 있는 값이 하나의 flat한 값으로 나오게 되는 것이다.

• 또한 하나가 아닌 다수의 필터가 있다면, 여러 개의 유닛을 입력으로 받아서 한 조각으로 묶는 셈이 되고, 출력은 6x6가 필터의 수만큼 있게 된다.
• 즉, 완전 연결 신경망을 36개의 위치에 각각 적용하여, 이 숫자들을 입력값으로 받고 필터의 수 만큼 출력하는 것이다.

1x1 합성곱은 언제 유용한가?

• 만약 우리가 너비나 높이를 줄이고 싶다면, 풀링층으로 사용하면 된다.
• 이와 비슷하게, 만약 채널의 개수를 줄이고 싶다면 이 1x1 합성곱을 사용해주면 되는 것이다.

• 만약 32개의 1x1x192 필터를 갖는 합성곱을 해준다면, 이 필터의 개수만큼의 채널로 줄어들게 된다.
• 또한 이 1x1 합성곱 층은 비선형성을 더해주고, 또 하나의 층을 더해줌으로써 더 복잡한 함수를 학습할 수 있게 해준다.

즉, 이 1x1 합성곱 층을 사용하면, (1) 채널의 개수를 줄일 수 있고, (2) 비선형성을 더해주고, (3) 또 하나의 층을 더해줌으로써 더 복잡한 함수를 학습하게 해준다.

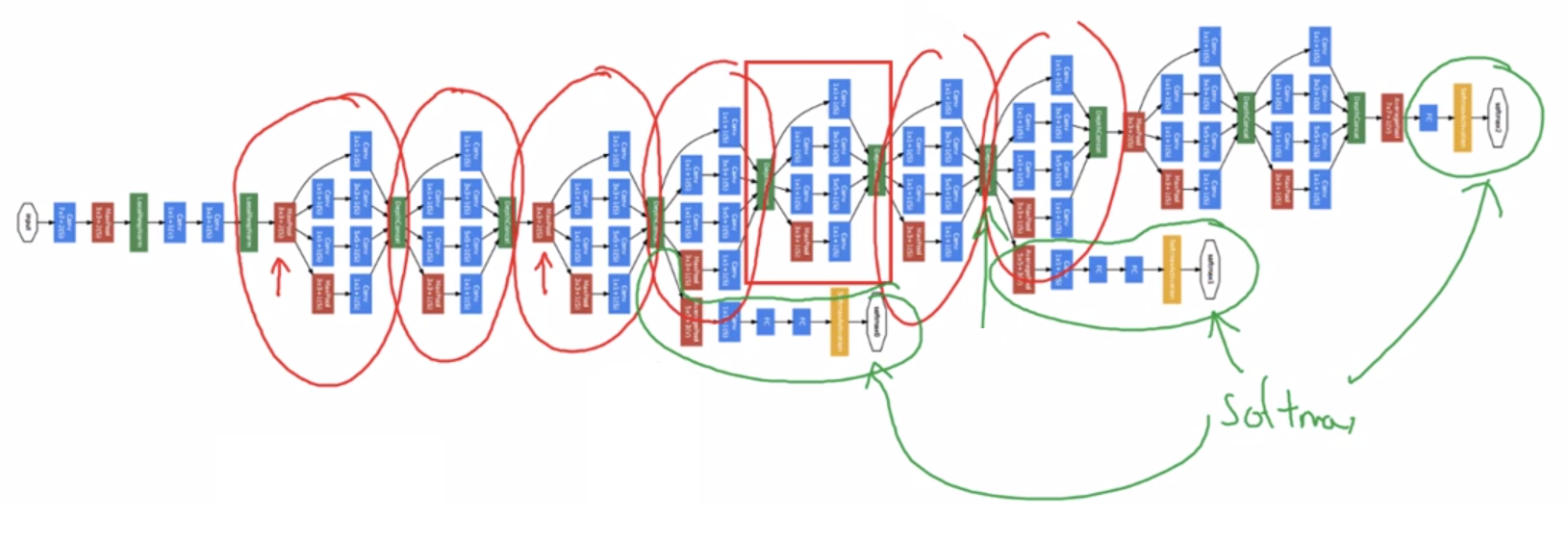
Inception 네트워크

• 만약 합성곱 층을 사용하게 된다면, 필터의 크기를 1x1로 할지, 3x3, 5x5로 할지 등을 결정해야하고, 또 풀링 층을 사용할지도 결정해야한다.
• 인셉션 네트워크는 위 필터들과 풀링 층 결정하는 대신, 모두 사용한다.
• 이 네트워크는 복잡해질 수는 있지만 훨씬 더 좋은 성능을 갖게 된다.

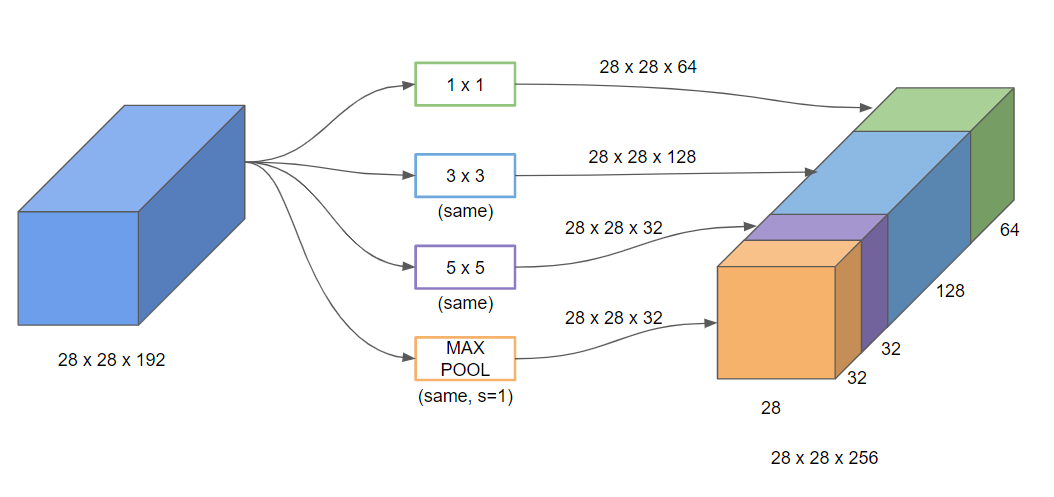
• 만약 28x28x192 입력값이 있다고 해보자.
• 여러개의 사이즈를 갖는 필터들을 동일한 합성곱에 다 사용하고 풀링 층까지 사용해서, 각각의 결과를 쌓아준다.
• 이렇게 하면, 네트워크가 학습하는 동안 더 효과적인 조합을 알아서 추출하게 되는 것이다.

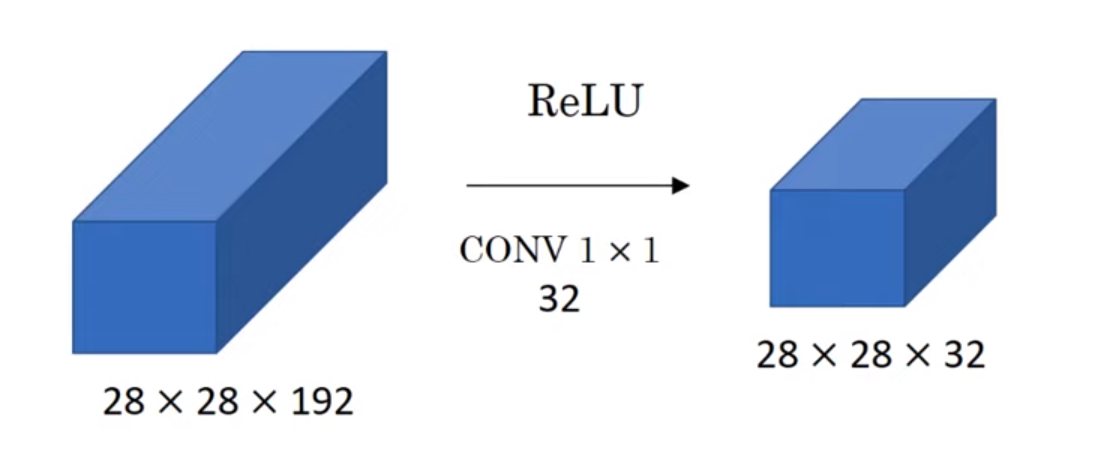
계산 비용에 대한 문제 해결 : Bottleneck Layer

• 모든 필터 사이즈들을 다 합쳐서 계산하는 것이기 때문에, 당연히 계산 비용에 대한 문제가 발생할 수 밖에 없다.
• 그렇기 때문에 이 문제를 해결하기 위해, 우선 1x1 합성곱을 해서 채널의 개수를 줄인 후 합성곱을 해주면 더 적은 계산을 할 수 있게 된다.

• 만약 중간에 1x1 합성곱 층이 없고 바로 5x5 필터를 적용한 합성곱을 했다면 (5x5x192) x (28x28x16) = 약 1억 2천만개의 계산을 해야했을 것이다.
• 하지만 차원을 축소하여 28x28x16 입력차원을 우선 만들어줬기 때문에 (28x28x16) x 192 + (28x28x32) x (5x5x16) = 240만 + 1천만으로 훨씬 더 적은 계산으로 같은 차원의 출력값을 계산할 수 있게 되는 것이다.
• 이 1x1 합성곱을 병목 층 Bottleneck Layer이라고 부른다.

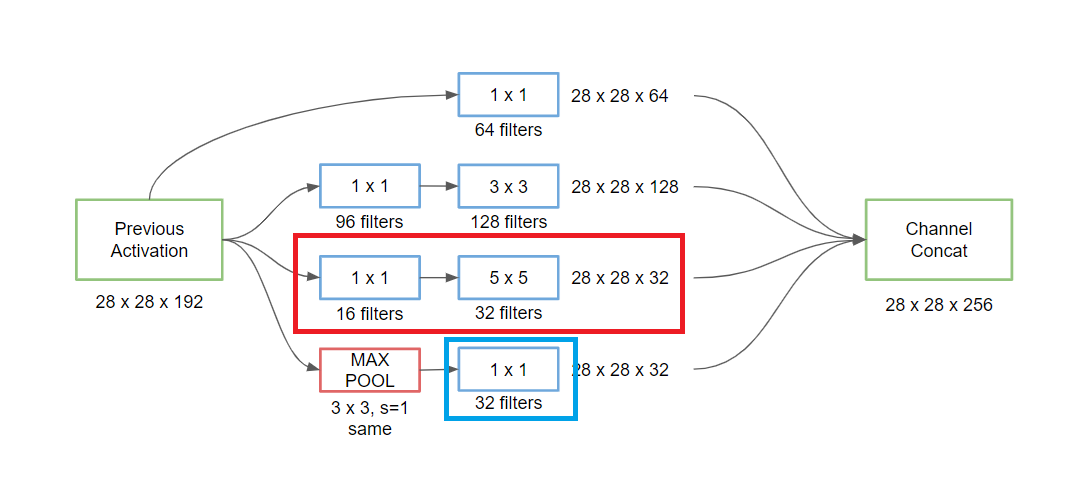
Inception 네트워크의 구조

• 아래 빨강색 부분은 위 예시와 같이 병목 층을 사용해서 차원의 개수를 줄인 후 5x5 합성곱 층을 적용해준 것이다.
• 이와 비슷하게 3x3 합성곱 층에도 병목 층을 먼저 사용해준 후 계산해준다.
• 풀링 층을 적용할 경우, 채널의 개수가 너무 많아지기 때문에 1x1 합성곱 층으로 채널의 개수를 줄여준다.
• 이 모든 결과들을 다 연결 concatenate 시켜준다면, 28x28x(64+128+32+32)의 차원을 갖는 출력값을 갖게 된다.

• 이렇게 위 예시가 하나의 인셉션 모듈이 되는 것이다.
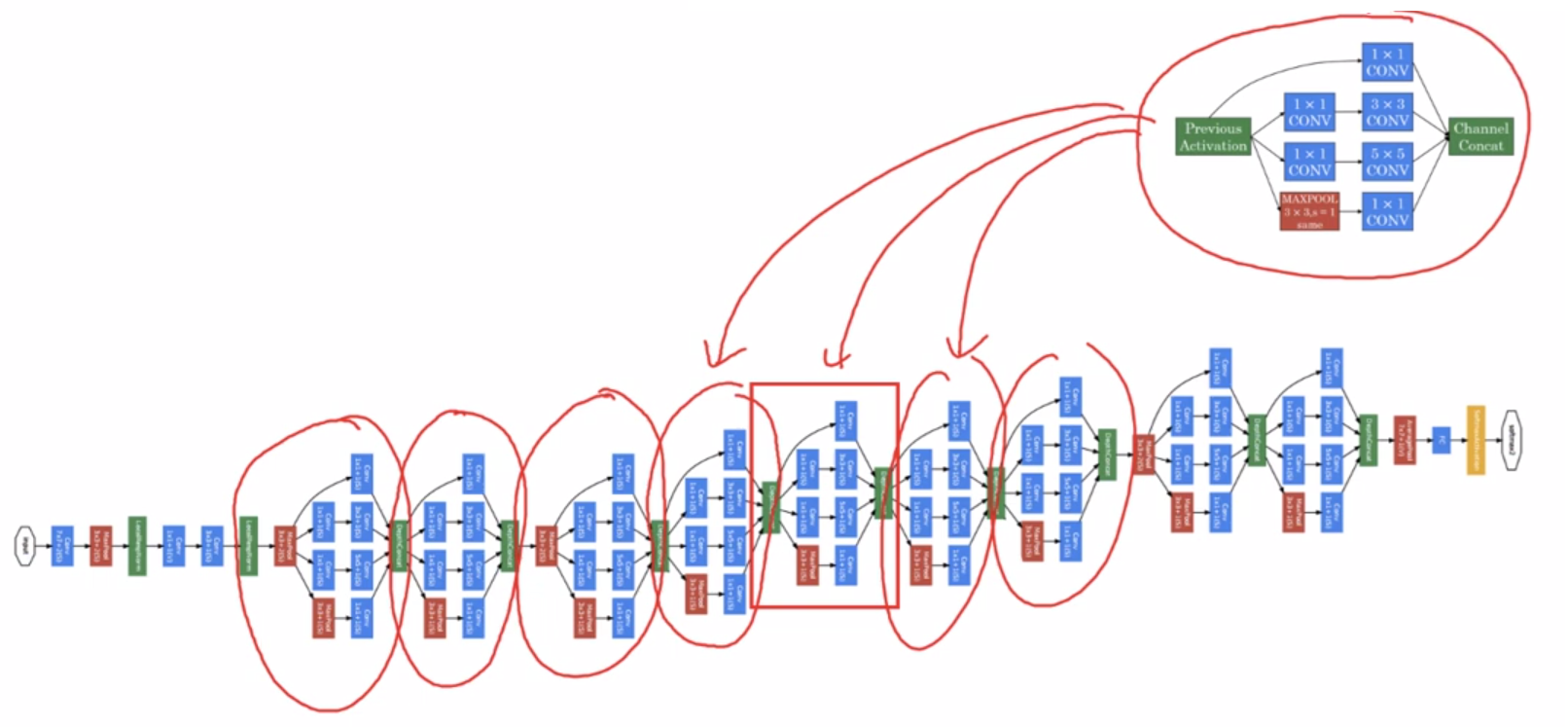
• 이 인셉션 모듈들을 합치면 아래 사진처럼, 하나의 인셉션 네트워크가 되는 것이다.
• 즉 인셉션 모델은 이 인셉션 모듈들의 합과 같다.

• 또한 인셉션 네트워크에는 중간중간에 소프트맥스를 계산하는 곁가지 side branches들이 있다.
• 이 곁가지들은 인셉션 네트워크의 도중에도 어느정도 좋은 결과가 나온다는 것을 보장하며, 정규화 효과를 주고 과대적합을 방지한다.