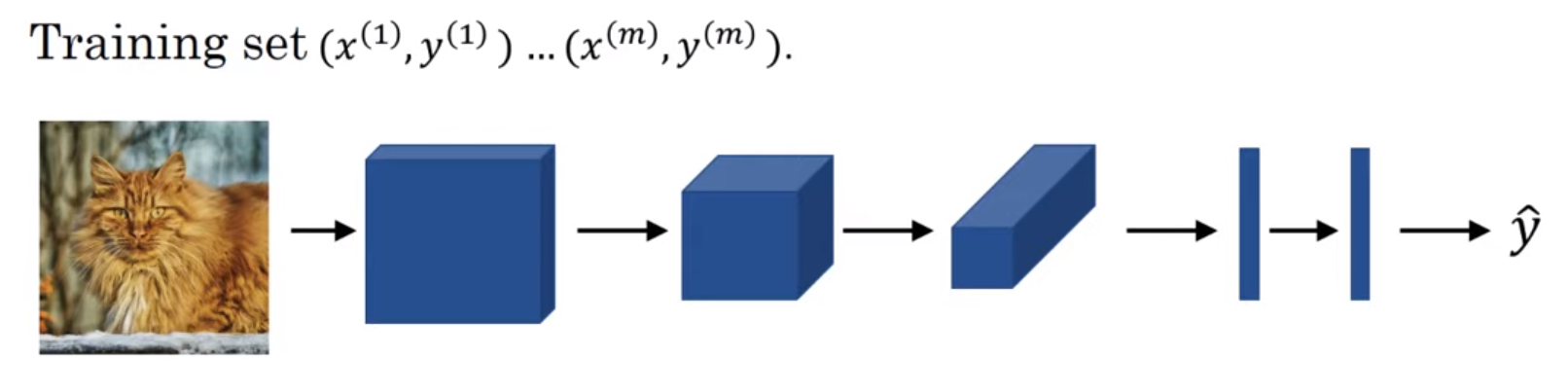
12 합성곱 신경망

컴퓨터 비전

• 컴퓨터 비전은 이미지 분류, 객체 인식, 신경망 스타일 변형 등이 있다.
• 컴퓨터 비전의 장애물 중 하나는 입력이 매우 커질 수 있다는 것이다.
  • 만약 64x64 컬러 이미지를 사용한다면, 총 64x64x3=12288개의 데이터를 갖게 될 것이다
  • 하지만 64x64는 매우 작은 이미지이며, 1000x1000 컬러 이미지를 분석하게 된다면 300만개의 데이터를 갖게 된다.
  • 이렇게 큰 데이터를 학습하게 된다면, 각 층의 갯수가 많아져 변수의 수도 많아질 것이고, 이런 경우 과적합을 방지하는 것이 어려워질 것이다.
• 이 단점들을 보안하기 위해서 합성곱 신경망을 사용하는 것이다.

모서리 감지 예시

• 합성곱 작업은 합성곱 신경망에 핵심 요소이다.

• 모서리 감지를 통해 합성곱이 어떻게 작동하는지 알아볼 것이다.

• 이전 영상에서는 신경망의 하위 층이 모서리를 감지하고 이후 층들이 가능성있는 물체를, 또 이후 층들이 물체의 부분을 인식하게 했었다.

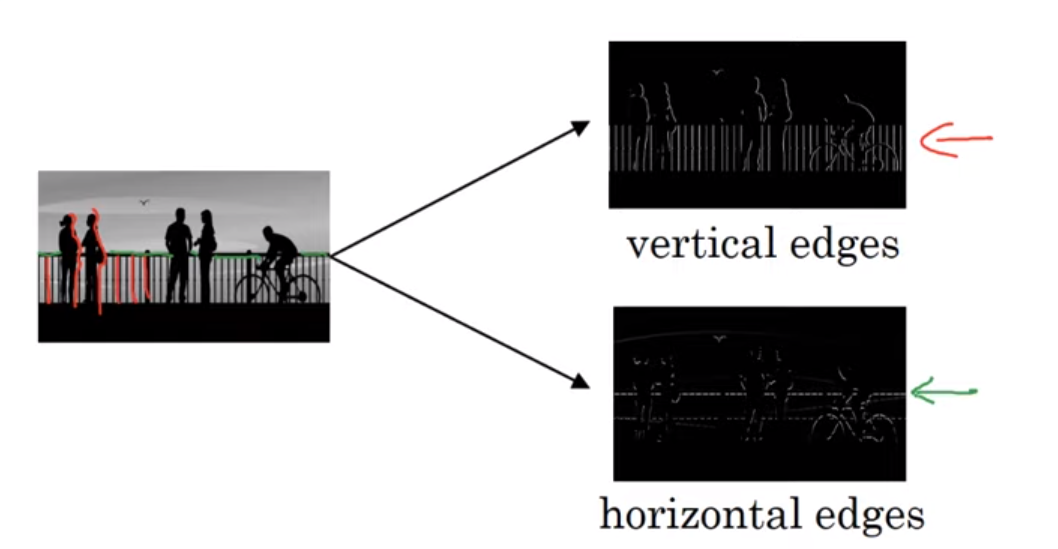
• 만약 위 이미지를 컴퓨터가 인식한다고 해보자
• 그렇다면 컴퓨터는 세로선들과 가로선들을 인식하게 될 것이다.

• 이렇다면 이런 이미지에서 모서리는 어떻게 감지하는걸까?

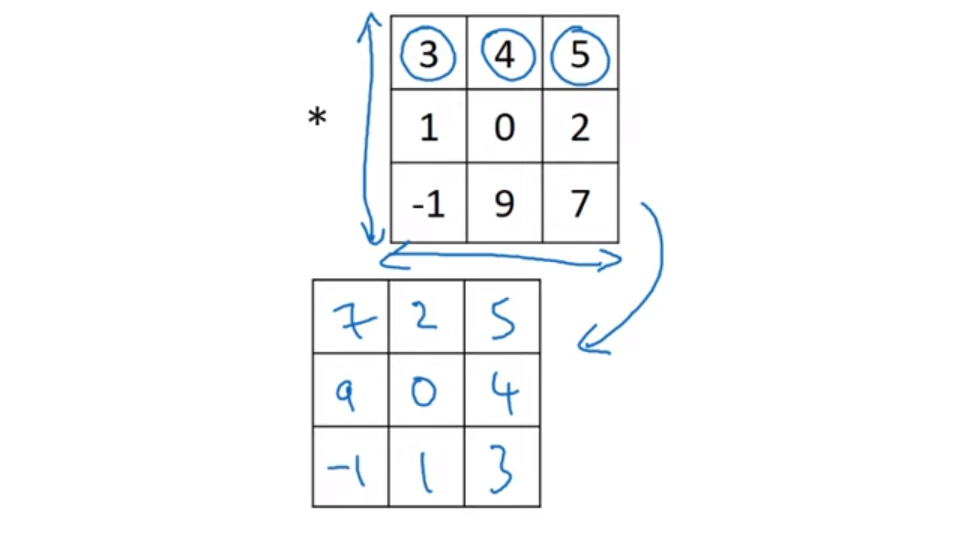
• 6x6 흑백 이미지가 있다고 해보자
• 그리고 3x3 크기에 “필터 filter” 또는 “커널 kernel”이 있다
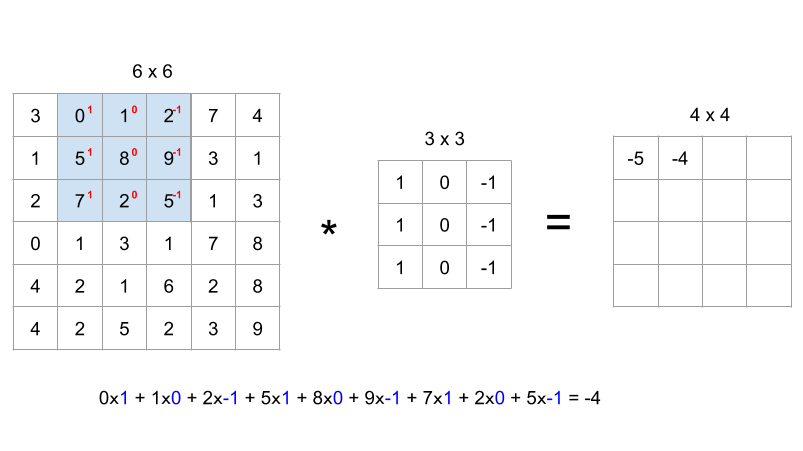
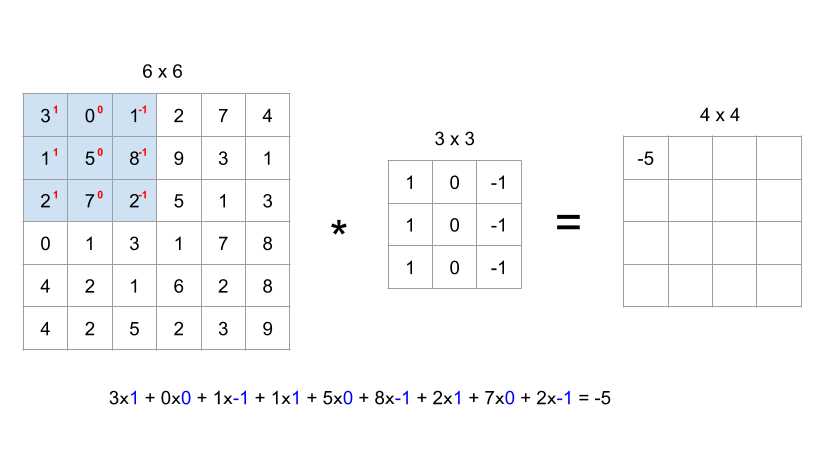
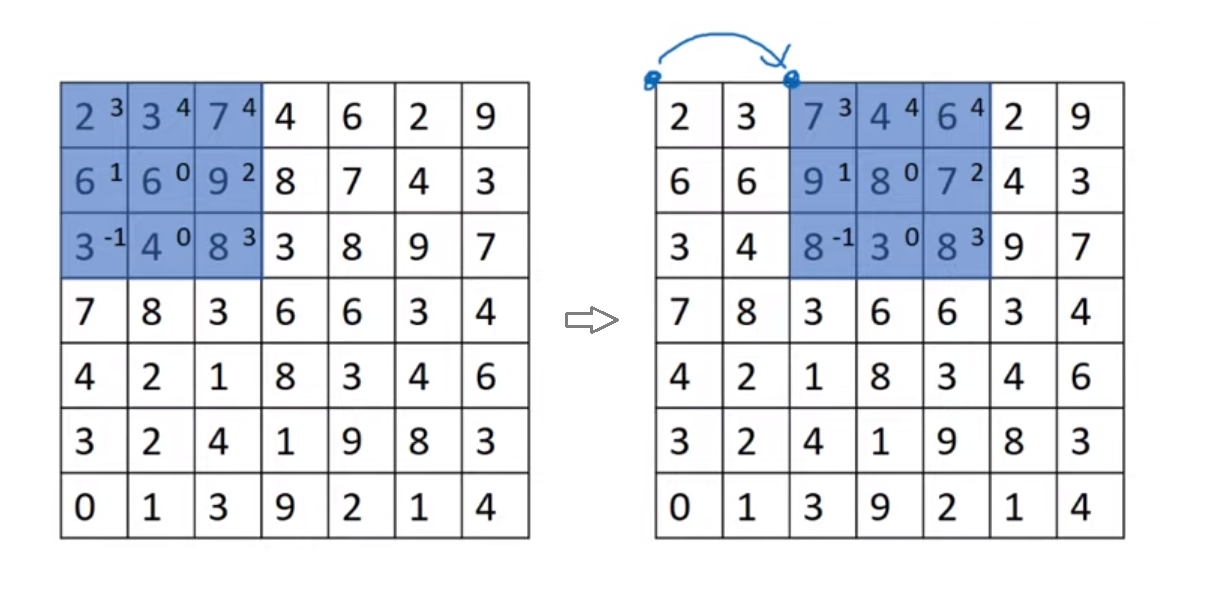
• 이 이미지와 필터의 합성곱(convolution)을 구하면 4x4 matrix가 생성되게 된다.

• 위 사진은 4x4 행렬의 첫 번째 요소를 계산하는 방법이다.
• 6x6 이미지에 필터값을 올려놓고, 대응하는 값들에 대한 곱셈을 하여 더해주면 첫 번째 요소값이 나오게 된다.

• 이후 다음 요소를 계산하기 위해 이 필터를 옮겨 똑같이 element-wise product를 구해준다.
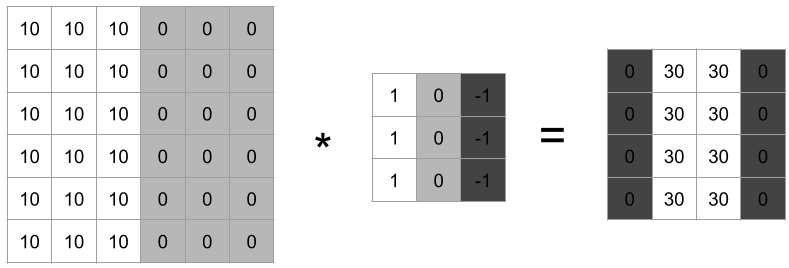
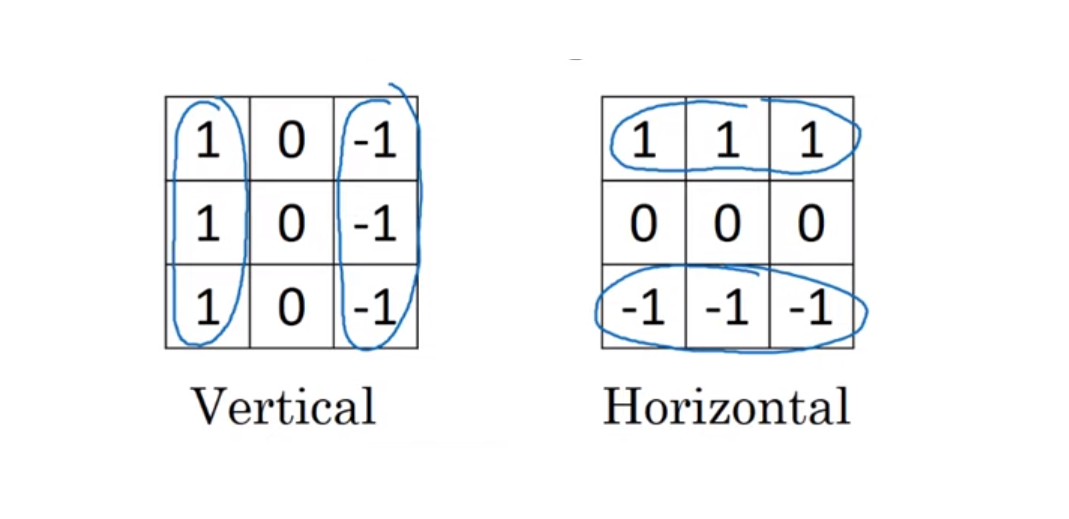
• 이 필터는 수직 윤곽선을 감지하기 위한 필터이다.

수직 윤곽선 감지

• 0에 가까울수록 어두워지고 값이 커질수록 밝아진다.
• 왼쪽 행렬에 위 필터를 적용시킨다면 오른쪽과 같은 결과가 나오게 될 것이다.
• 이 오른쪽의 결과는, 이 경계가 명확하게 표현되는 이미지를 얻게 된다.
• 이 예시에서는 경계가 두껍게 표현된 것 같지만, 만약 더 큰 이미지를 합성곱 신경망에 학습시킨다면 더 정교한 결과를 얻을 수 있을 것이다.
• 수직 경계선 컴출에서 3x3 필터의 완쪽에는 밝은 값이 있고, 오른쪽에는 어두운 픽셀이 있다. 그렇기 때문에 경계선이라고 확신할 수 있게 되는 것이다.

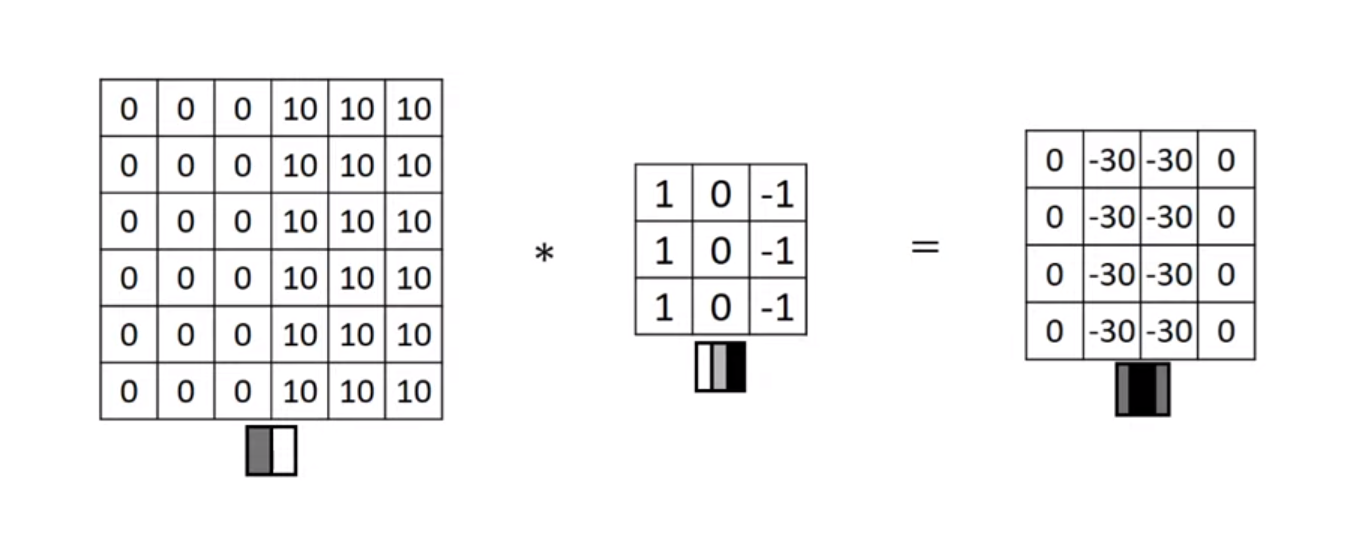
• 만약 위 예시의 6x6 이미지를 좌우반전하여 같은 필터에 적용해본다고 하면, 결과 행렬의 값이 반전(invert)되어있을 것이다.
• 만약 이 값의 차이가 상관 없다면, 이 결과값에 절대값을 씌우면 될 것이다.
• 하지만 중요한 것은, 이 필터는 밝은 곳에서 어두운 곳으로 가는 것과 그 반대의 경우의 차이를 알려준다.

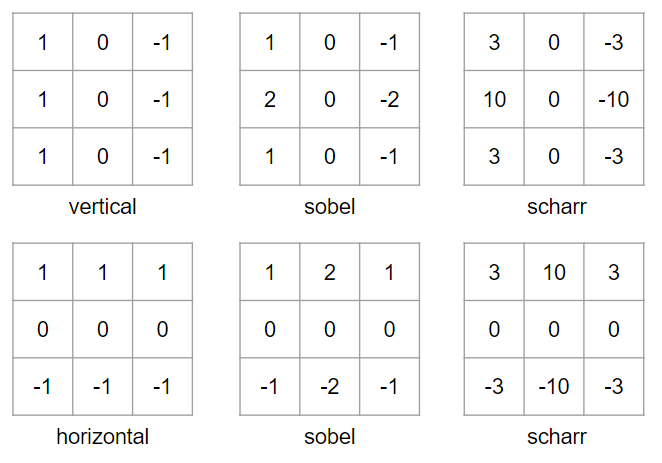
다양한 필터들

• 수직 윤곽선 : 오른쪽은 상대적으로 밝고 왼쪽은 상대적으로 어둡다.
• 수평 윤곽선 : 위쪽은 상대적으로 밝고 아래쪽 상대적으로 어둡다.

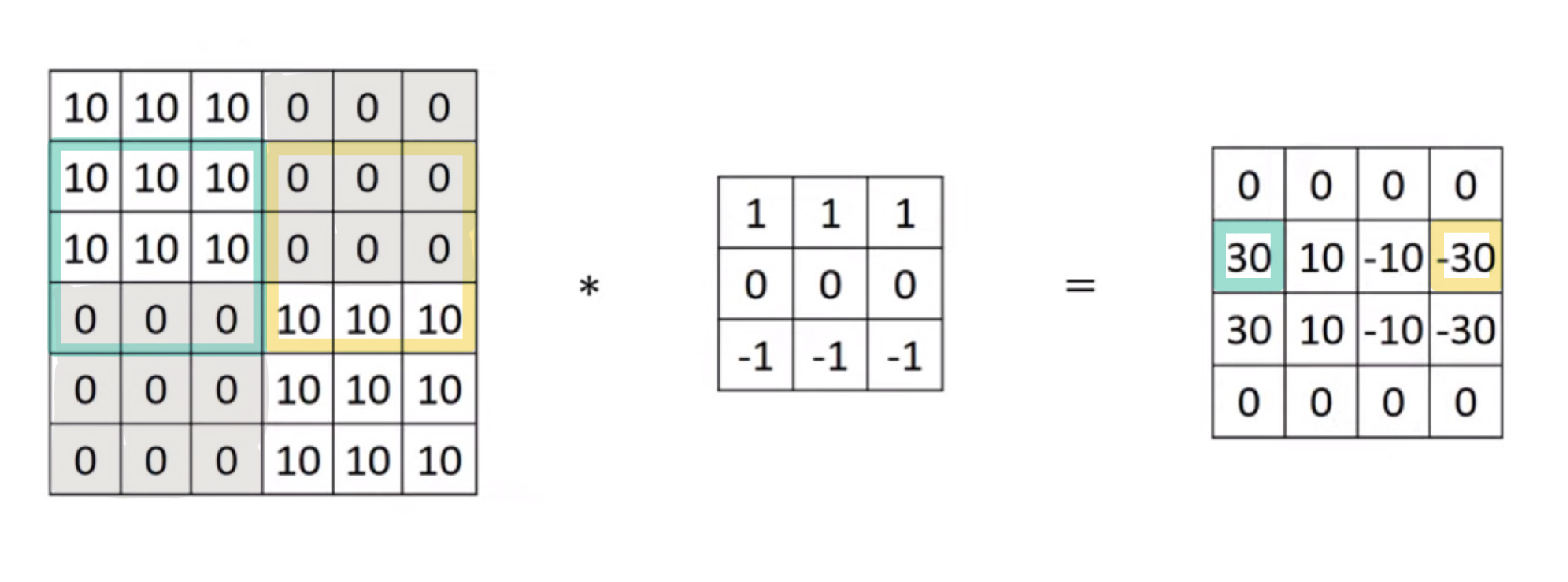
• 이 이미지에 수평 윤곽선 필터를 적용했을 때, 초록색 부분의 윗 부분은 밝고 아랫 부분이 어둡기 때문에 강한 양의 윤곽선을 보여준다.
• 노랑색 부분은, 아랫부분은 밝고 윗 부분은 어둡기 때문의 음의 윤곽선을 나타낸다.
• 중간에 10과 -10이 있는 이유는, 밝은 부분의 일부분과 어두운 부분의 일부분 모두를 대표하고 있기 때문에 중간 크기의 값이 나온 것이다.
• 하지만 만약 이 같은 이미지가 1000x1000로 더 많은 픽셀을 갖고 있다면 이 애매한 부분이 상대적으로 작아서 눈에 띄지 않을 것이다.

💡 서로 다른 필터는 세로 또는 가로의 윤곽선을 검출해낸다.

• 컴퓨터 비전에서는 그동안 어떤 숫자들을 필터로 사용할지에 대한 논쟁이 계속 있었다.
• 아래 사진은 그동안 사용했던 필터들이다.

딥러닝을 통해 필터값 학습

• 하지만 딥러닝이 발전하면서 우리는 어떤 복잡한 이미지에서 윤곽선을 검출하려고 할 일일히 이 필터의 값들을 정할 필요가 없다는 것을 알아냈다.
• 필터의 값들을 파라미터로 설정하여 학습을 통해 가장 효과적인 윤곽선 검출기의 값들 정하면 된다.

패딩 Padding

💡 패딩을 넣어주는 목적

아래 단점들을 보완하기 위해서 원본 이미지에 패딩을 넣어준다.

합성곱의 단점들

1. 이미지의 축소
   • 전 예시들에서는 6x6 이미를 3x3 필터를 거침으로서 4x4 행렬을 얻게 된다.
   • 이 결과 행렬을 위한 계산은 이렇다 : $n-f+1$
   • 즉, 합성곱을 통해 계산을 하면 이미지가 축소된다는 것을 알 수 있다.
2. 픽셀의 중요도
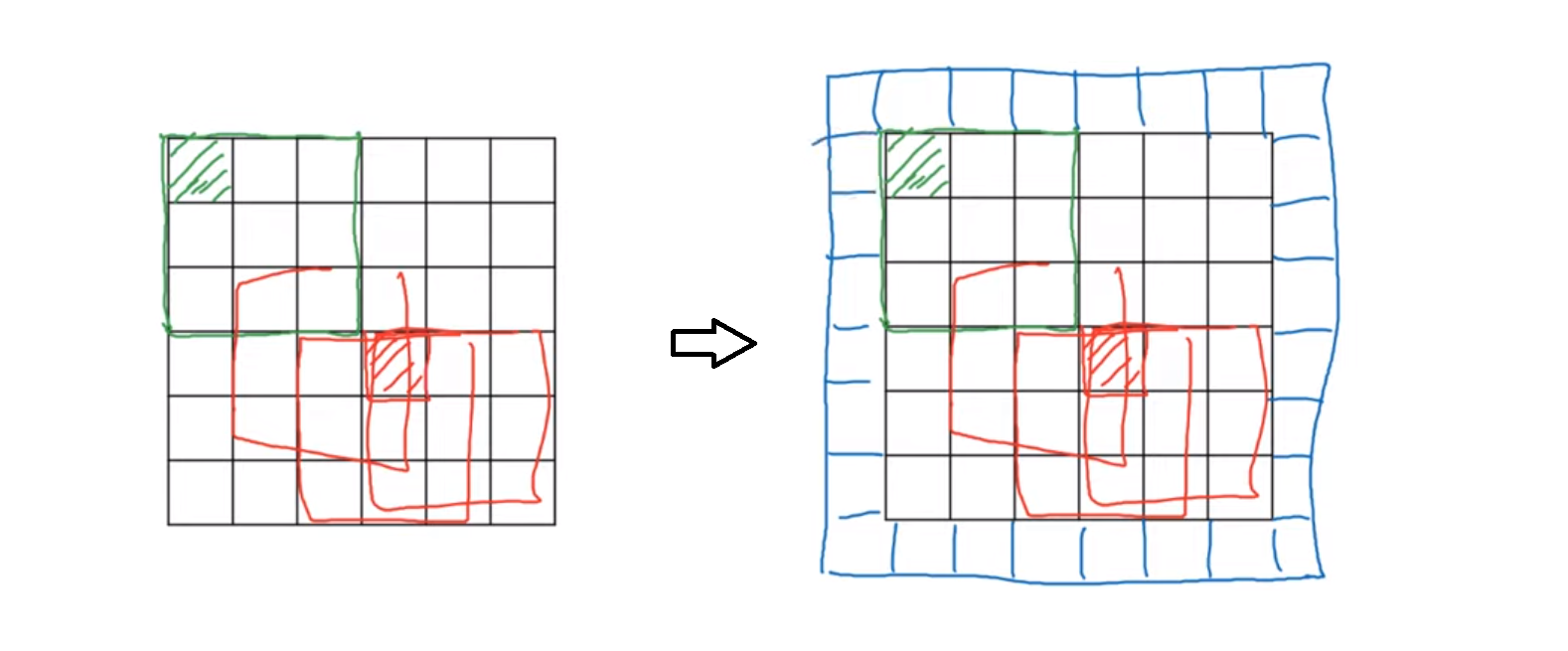
   • 아래 초록색으로 표시된 가장 위에 있는 픽셀은 필에서 단 한번만 통과된다.
   • 빨강색으로 표시된 중간에 있는 픽셀은 필터를 여러번 통과한다.
   • 그렇기 때문에 이 픽셀의 위치에 따라 각 픽셀의 중요도가 달라진다는 것을 알 수 있다.

• 보통 패딩은 숫자 0을 사용한다.
• 패딩을 넣어준다면, 이제 6x6 이미지가 아닌 8x8 이미지가 된다.
• 행렬을 위한 계산을 이렇다 : $n+2p-f+1$
• 그렇게 된다면 결과 행렬이 6x6이 되어 원본 이미지의 사이즈를 보존할 수 있게 되는 것이다.
• 또한 패딩을 1개가 아닌 $p=2$인 패딩을 넣을 수도 있다.

유효 합성곱과 동일 합성곱

유효 합성곱 (valid convolution)

• 패딩이 아예 없는 것
• $n-f+1$

동일 합성곱 (same convolution)

• 기존 이미지의 픽셀 사이즈와 결과 이미즈의 사이즈가 같도록 패딩을 넣어주는 것
• input size = output size
• $n +2p-f+1$ where $p=\frac{f-1}{2}$

필터의 사이즈 설정

컴퓨터 비전에서는 대부분 필터의 사이즈 $f$는 홀수이다. 대부분 3x3, 5x5 또는 7x7이다.

1. 만약 $f$가 짝수라면, 패딩이 비대칭이 된다. $f$가 홀수여야만 합성곱에서 동일한 크기로 패딩을 더해줄 수 있다. 짝수라면 왼쪽과 오른쪽이 서로 다르게 패딩을 해줘야한다.
2. 만약 $f$가 홀수라면, 중심위치가 존재한다. 컴퓨터 비전에서는 구별된 중심 픽셀이 존재하는 것이 유리하다.

스트라이드 Stride

아래는 스트라이드가 2일 때의 예시이다.

• 스트라이드가 2라는 것은 필터가 이동할 때 바로 옆으로 움직이는 것이 아닌, stride만큼 움직인다는 것을 의미한다.
• 또한 스트라이드는 출력 이미지의 사이즈에도 영향을 미친다.
• 출력 이미지의 사이즈의 계산은 이렇다 : $\frac{n+2p-f}{s}+1$
• 위 예시는 $n=7, s=2$이기에 최종 결과의 행렬의 사이즈는 3x3가 될 것이다.
• 또한 만약 위 분수의 값이 정수가 아니라면 내림을 해준다.
• 최종적으로 출력 이미지의 사이즈는 아래와 같게 된다.

\[\lfloor{\frac{n+2p-f}{s}+1} \rfloor\]

교차상관 Cross-correlation vs. 합성곱 Convolution

💡 수학적으로 정의되는 합성곱과 딥러닝에서 사용하는 합성곱의 차이가 존재한다.

• 수학의 합성곱에서는 요소들을 곱하고 더하는 계산을 하기 전에, 필터를 좌우반전과 상하반전, 즉 미러링을 해준다.

• 우리가 지금까지 정의한 합성곱은 이 미러링을 건너뛰고 있었다.
• 이 “미러링을 건너뛴 합성곱”은 교차상관이라고 불린다.
• 하지만 대부분의 딥러닝 관련 문헌들은 이 교차상관을 대부분 합성곱이라고 칭하고 있다.

**입체형(컬러) 이미지에서의 합성곱**

• 이미지에 색상이 들어가면 입체형을 변하게 되어 차원이 증가하며 채널이 생긴다.
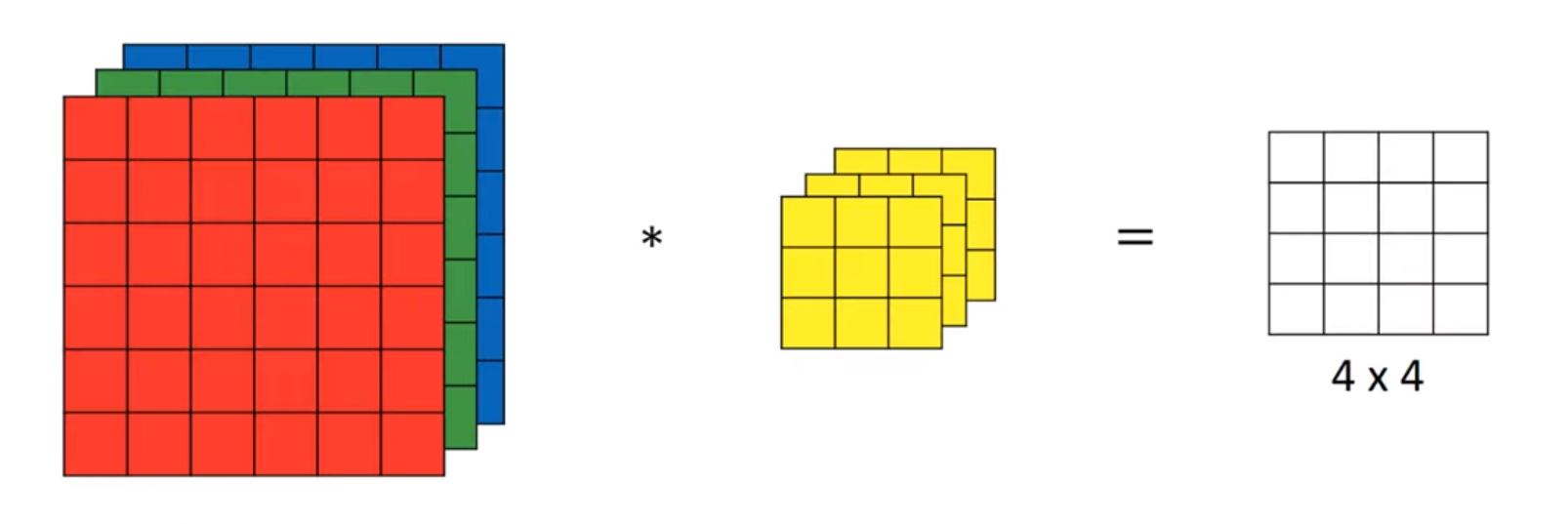
• RGB 컬러일 경우 $n\times n\times3$ (즉, 높이 x 넓이 x 채널) 이미지다.
• 필터도 동일한 개수의 채널을 갖게 된다 : $f\times f \times 3$

• 만약 빨간색 채널의 세로 윤곽선을 구하고자 하면, 빨간색에 대응하는 채널만 값을 갖고 나머지 채널들은 0 값을 갖게 할 수 있다.
• 또한 색이 상관없으면 모든 채널들에 대응하는 필터들이 세로 윤곽선 필터값들을 갖게 된다.
• 즉, 이렇게 각 색의 채널들에 대해 다른 값을 넣게 되면서 각 채널에 대해 따로 알아볼 수 있게 된다.
• 또한 이런 3D 데이터에 합성곱을 적하면 2D 행렬이 나온다.

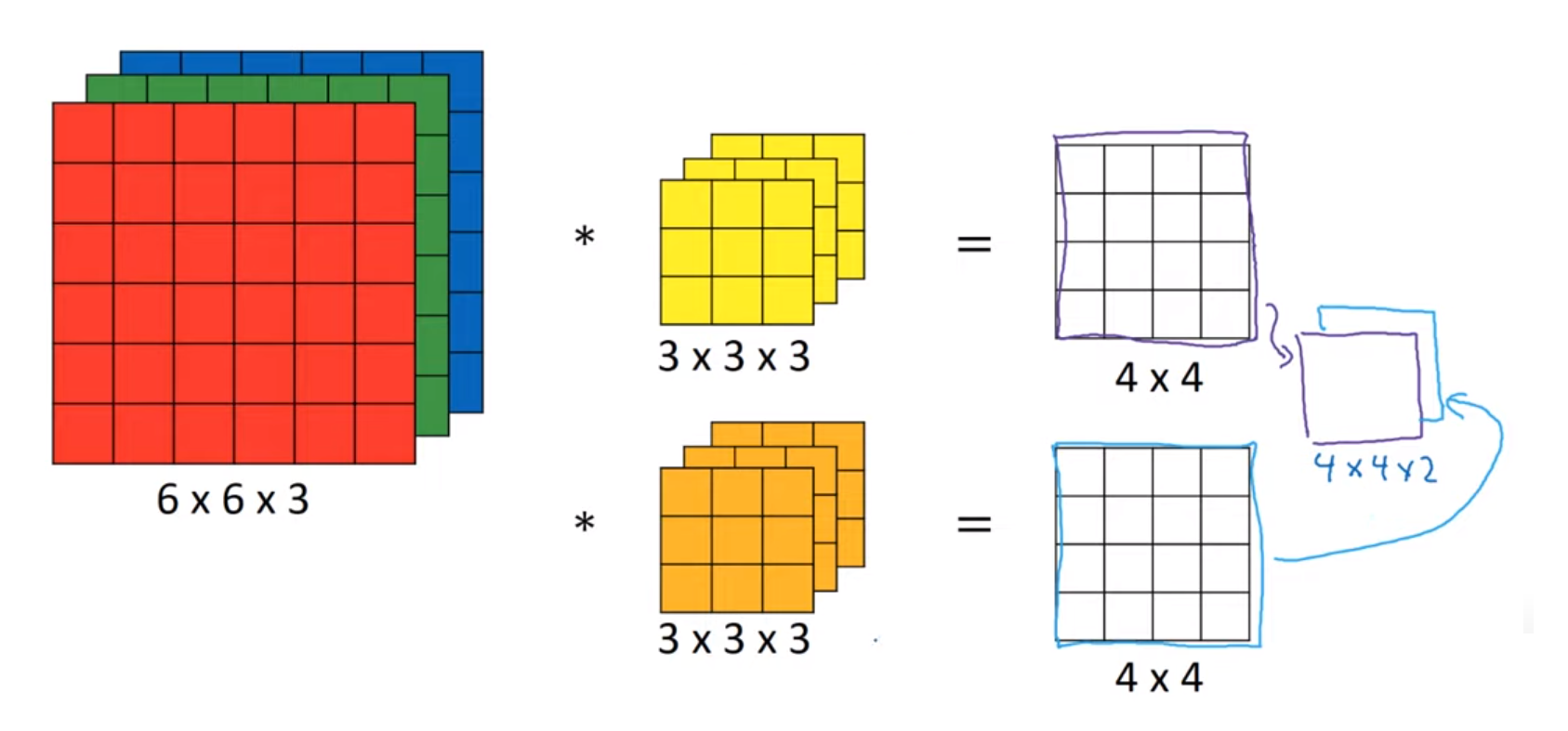
여러 개의 필터를 동시에 사용

• 만약 세로 윤곽선 필터와 가로 윤곽선 필터를 동시에 사용하고자 하면 어떻게 하면 될까?

• 위 그림처럼, 여러개의 필터를 사용하여 나온 값들의 결과를 하나의 결과로 합쳐서, 결과 행렬이 부피를 얻게된다.

• 패딩과 스트라이드가 없다고 가정했을 때, 최종 출력으로 아래의 형태가 출력이 된다.

  \[(n \times n \times n_c) * (f \times f \times n_c) = (n-f+1) \times (n-f+1) \times n_c\prime\]
  • $n :$ 이미지의 크기
  • $n_c :$ 채널의 개수
  • $f :$ 필터의 크기
  • $n_c\prime :$ 사용된 필터의 개수

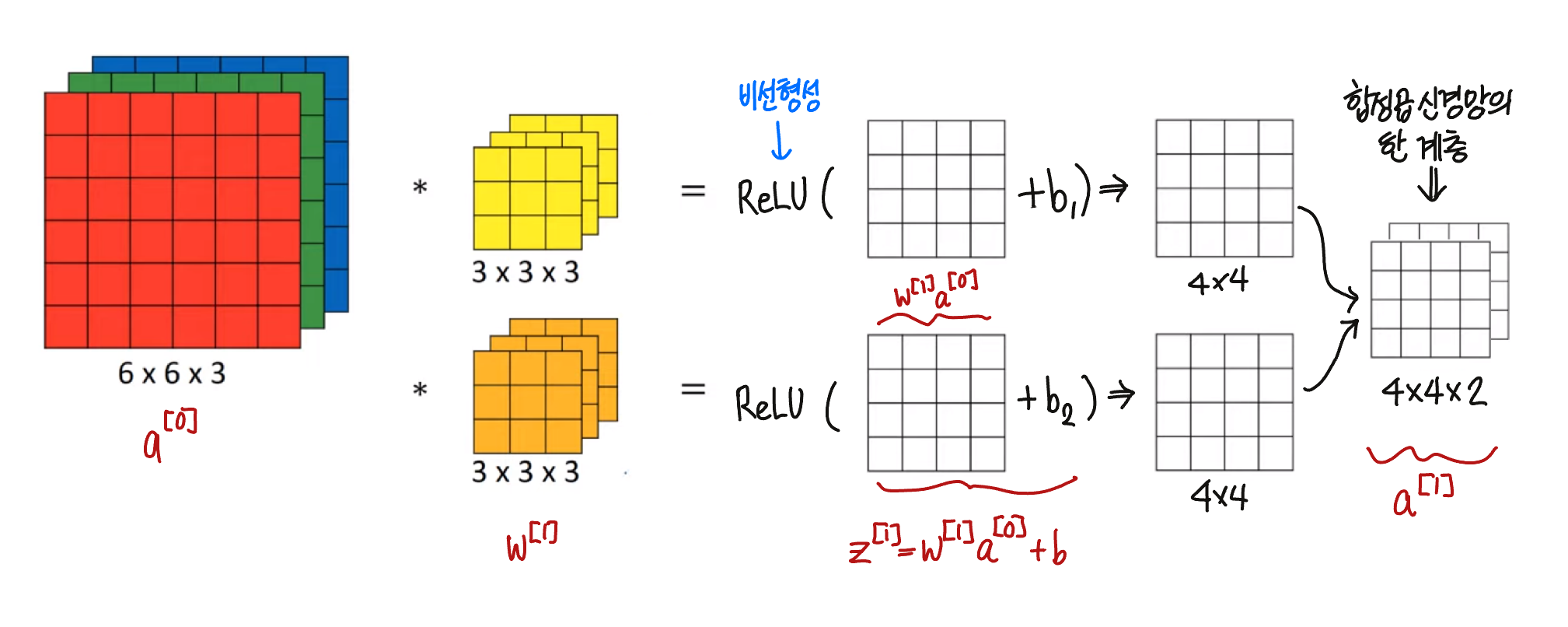
합성곱의 한 계층 구성하기

• 우선 합성곱을 해준다. 여기서 결과물은 4x4 2차원 행렬이며, 이 행렬에 편향 $b$을 더해준다. 이 값은 그동안 신경망을 공부하면서 배웠던 $z^{[1]} = w^{[1]}a^{[0]}+b$ 를 계산하는 것과 유사하다.
  • $a^{[0]}$은 학습할 이미지, $w^{[1]}$는 필터를 의미한다.
• 이 값에 ReLU와 같은 활성화 함수를 통해 비선형성을 더해준디
• 각 필터에 같은 계산을 반복하여, 이 채널들을 더해주면 최종적으로 합성곱 신경망의 한 계층인 4x4x2 2차원 행렬이 나오게 되며, 심층 신경망의 $a^{[1]} = g(z^{[1]})$ 와 유사하다.

한 계층의 파라미터 개수

만약 10개의 3x3x3 필터가 신경망의 한 계층에 있다면, 해당 계층의 파라미터의 개수는 무엇일까?

• 한 필터는 3x3x3이다. 즉, 각 필터는 27개의 파라미터를 갖고 있다.
• 편향을 더해준다면 총 28개의 파라미터가 된다
• 이 필터가 10개가 있다면, 28x10, 총 280개의 파라미터를 갖게 된다.

여기서 좋은 점은, 원 이미지의 사이즈가 6x6이던 1000x1000이던 같은 숫자의 파라미터를 같게 되어 이미지의 사이즈와 무관하게 과적합을 방지할 수 있다.

표기법

$f^{[l]} =$ 필터 사이즈

❓ 필터는 항상 정사각형이어야하나? The square filter is often selected just because there’s no preference in which direction a pattern can be found. For example, it can be a horizontal or a vertical line, both can be important features in an image and the network should capture any of those, if they are important. In other words, you might want your network to be symmetric. — source

$n_c^{[l]} =$ 필터의 개수

$p^{[l]} =$ 패딩 Padding 사이즈

$s^{[l]} =$ 스트라이드 stride 사이즈

입력 행렬, 즉 이전 층의 이미지 크기

• $n^{[l-1]}_H \times n^{[l-1]}_W \times n^{[l-1]}_C$

출력 행렬, 즉 현재 층의 이미지 크기

• $n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}$

$l$번째 층의 높이와 넓이의 크기 계산

• $n_H^{[l]} = \lfloor{\frac{n_H^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1} \rfloor$
• $n_W^{[l]} = \lfloor{\frac{n_W^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1} \rfloor$

각 필터의 크기

• $n_C^{[l]} = f^{[l]} \times f^{[l]} \times n_c^{[l-1]}$
• 필터의 채널 개수는 입력값의 채널의 개수와 같아야한다.

활성값의 개수 : 편향과 비선형성을 적용한 값

• $a^{[l]} = n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}$
• $A^{[l]} = m \times n_H^{[l]} \times n_W^{[l]} \times n_C^{[l]}$
• ❓여기서 $m$값은 예시의 개수

가중치의 개수 : 필터를 전부 모은 값

• $W^{[l]} = f^{[l]} \times f^{[l]} \times n_C^{[l-1]} \times n_C^{[l]}$
• 마지막 계층 $l$의 필터의 개수만큼 곱해준다.

편향의 개수

• $b = n_C^{[l]} = (1,1,1,n_C^{[l]})$
• 나중에는 이런 형태의 4차원 행렬로 나타내기도 한다는 것을 알 수 있다.

총 파라미터의 개수

• 가중치의 개수 + 편향의 개

간단한 합성곱 네트워크 예시

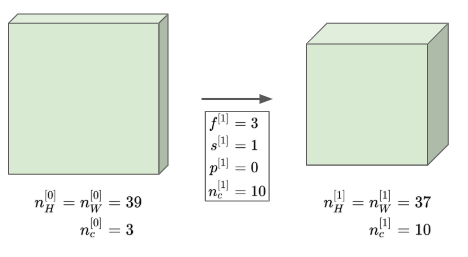
• 아래 사진의 오른쪽 상자가 입력되는 이미지라고 해보자
• 이 이미지는 39x39x3의 형태를 갖는 3차원 배열이다.
• 이 이미지를 $n_C=10$개의 3x3x3 형태의 필터를 통과시킨다.

• 그렇다면 결과 행렬은 37x37x10의 형태를 갖게 될 것이다
• 여기서 10은 필터의 개수에서 온 것이다.
• 우리의 표기법에 때르면, $n_H^{[l]} = n_W^{[l]} = 37$

• 이것이 첫 번째 층의 활성값이 된다.

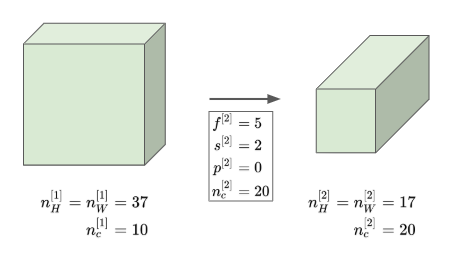
• 이제 이 결과에 다시 한번 더 합성곱을 진행한다.
• 여기서 필터의 개수는 5개, 그리고 스트라이드를 2로 바꿔준다.

• 결과 행렬은 17x17x20 행렬이 될 것이며, 두 번째 층의 활성값이 된다.
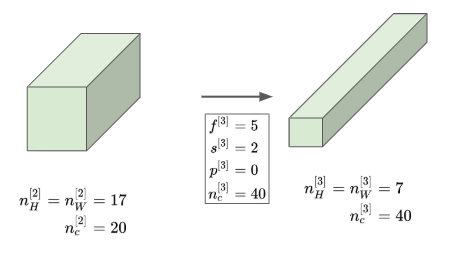
• 또 다시 5개의 필터를 스트라이드 2를 통해 다시 한번 더 합성곱을 진행하다.

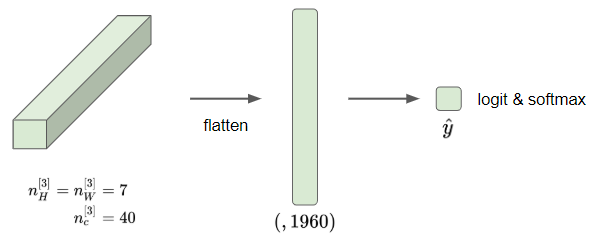
• 세 번째 층의 활성값은 7x7x40이 될 것이다.

그렇다면 39x39x3의 이미지로 7x7x40만큼의 특성을 계산한 것이다.

• 그리고 일반적으로 해주는 것은 이 활성값을 펼쳐서 7x7x40=1960개의 요소를 가진 하나의 벡터로 만들어준다.
• 이후 로지스틱 회귀 또는 소프트맥스 함수에 넣어주면, 이것이 신경망의 최종 예측값이 된다.

이것은 합성곱 신경망의 일반적인 예시이다.

하지만 합성곱 신경망을 만들 때 중요한 것은 필터의 크기나 스트라이드나 패딩의 크기 또는 필터의 개수와 같은 하이퍼파라미터를 성정하는데 있다.

가장 중요한 것은 아래와 같다

• 합성곱 신경망은 대부분 큰 사이즈의 이미지를 입력 받는다.
• 처음에는 이 크기가 유지되다가, 층이 깊어질수록 줄어든다.
• 반면 채널의 개수는 계속 늘어난다.

이 트렌드는 대부분의 합성곱 네트워크에서 확인할 수 있다.

세 종류의 층

1. 합성곱 층 Convolution Layer (CONV)
2. 풀링 층 Pooling Layer (POOL)
3. 완전 연결 층 Fully Connected Layer (FC)

풀링 층 Pooling Layer

풀링 층을 사용해 표현의 크기를 줄여 계산속도를 줄이고 특징을 더 잘 검출 해낼 수 있게 한다.

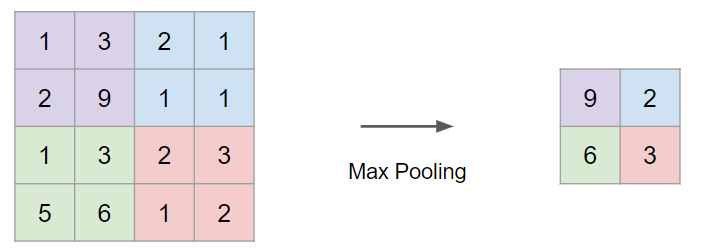
최대 풀링 Max Pooling

• 최대 풀링은 필터를 통과했을 때 해당 구역에서 가장 최대값을 뽑아내는 것을 의미한다.
• 최대 풀링의 하이퍼파라미터들은 $f$와 스트라이드 $s$이다. 아래 예시에서는 $f=2, s=2$ 이다.

• 만약 이 4x4 입력이 어떤 특성의 집합이라고 한다면, 여기서 최대값이 특정 특성을 의미할 수 있다.
• 만약 특정 특성이 존재한다면 큰 값이 남게 되는 것이고, 만약 특정 특성이 없다면 여전히 작은 수가 남게 되는 것이다.
• 하지만 결국 최대 풀링을 사용하는 이유는 최대 풀링을 사용했을 때 성능이 확실히 향상되기 때문이다.
• 또한 최대 풀링의 흥미로운 점은, 여러 하이퍼파라미터가 있지만 학습할 수 있는 변수가 없다는 것이다.

최대 풀링 예시

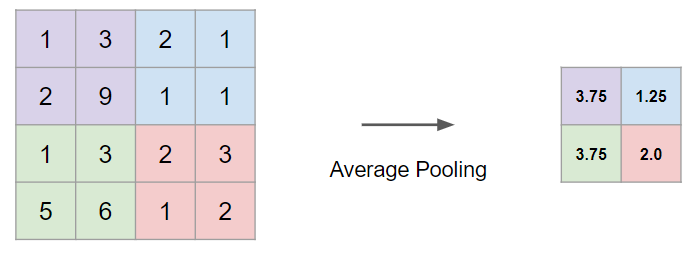
평균 풀링 Average Pooling

• 최대 풀링과 비슷하며, 최대값이 아닌 평균값을 구한다.
• 요즘에는 최대 풀링이 평균 풀링보다 많이 쓰인다.
• 하지만 예외는 있는데 매우 깊은 신경망에서 7x7x1000의 행렬을 1x1x1000 줄일 때 사용하기도 한다.

풀링 층의 하이퍼파라미

• $f$ : 필터 사이즈
• $s$ : 스트라이트
• max or average pooling
• $p$ : 패딩 (하지만 거의 사용하지 않는다)

풀링 층에는 역전파가 가능한 하이퍼파라미터가 없다

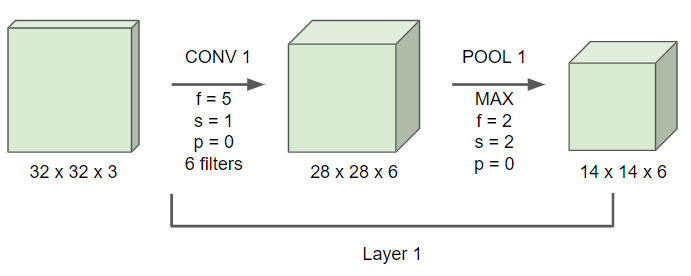
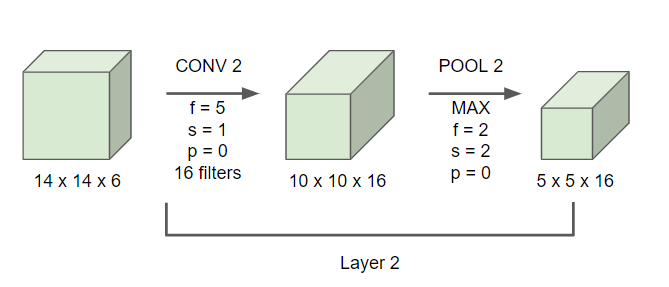
LeNet-5

• 하나의 합성곱 층 이후 최대 풀링을 적용해준다.
• 풀링을 적용함으로 이미지의 사이즈가 줄어들고, 채널의 개수는 유지된다.

합성곱 신경망에서는 2가지 관습이 있다.

1. CONV+POOL를 하나의 층으로 본다.
2. CONV와 POOL를 각각 다른 층으로 본다.

1번을 사용하는 사람들은 POOL 층은 하이퍼파라미터(가중치)가 없기 때문에 CONV층과 묶어서 하나의 층이라고 부른다.

해당 강의에서는 1번을 적용할 것이다.

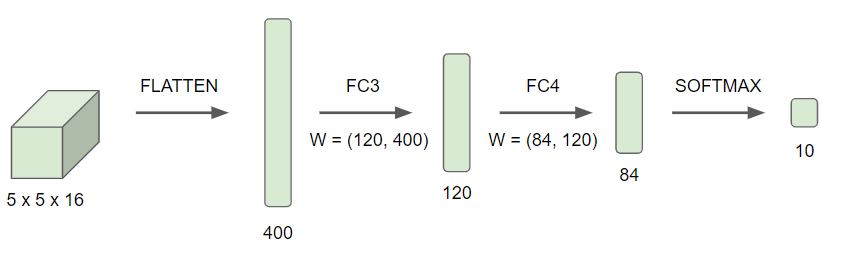
• 이 POOL2를 펼쳐서 400개의 유닛을 가진 벡터로 만들어준다.

• 이 벡터를 120개의 유닛을 가진 완전연결 (Fully Connected) 층으로 만들어준다.
• 다시 한번 더 완전 연결 층으로 만들어준 뒤 소프트맥스 함수를 적용시킨다.

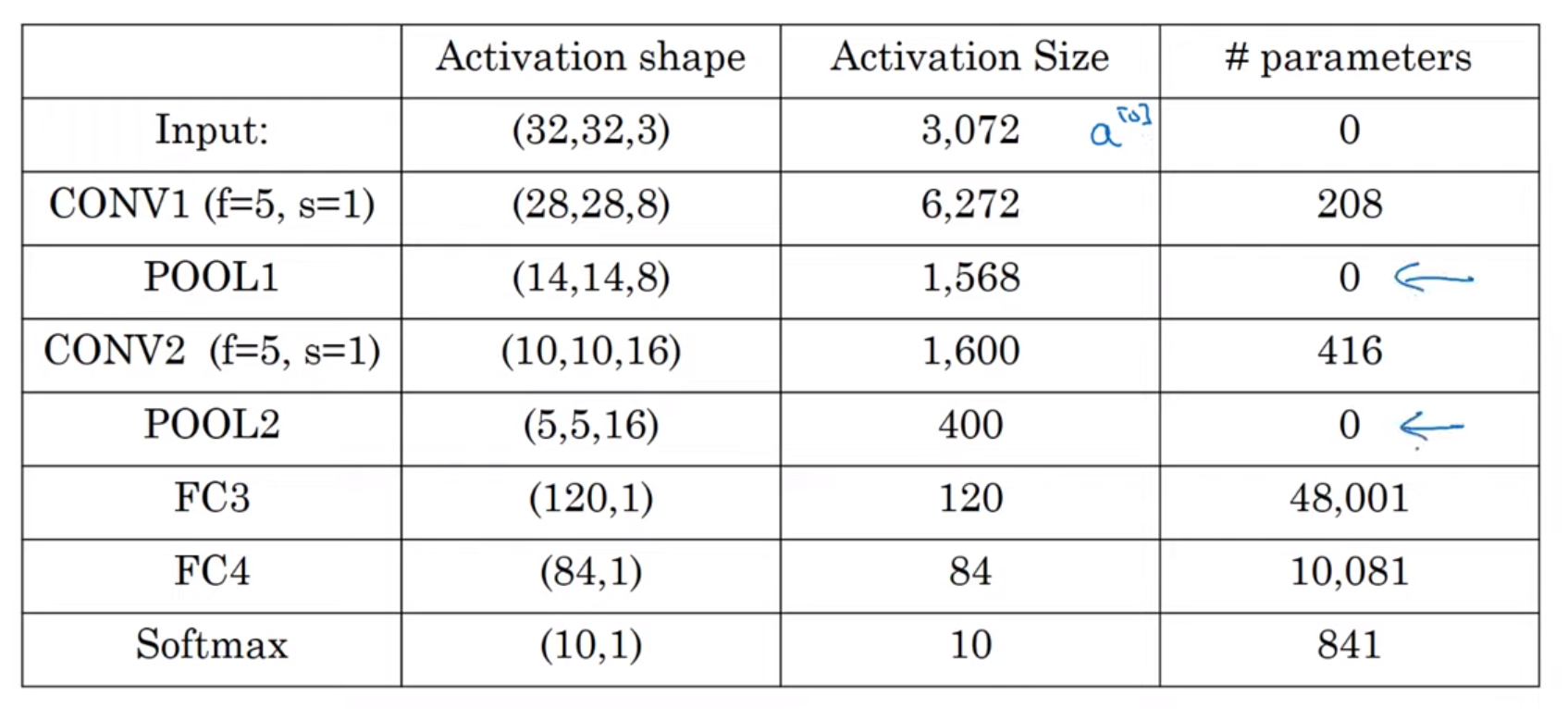
위 차트를 보고 주의 깊게 봐야할 패턴들은 아래와 같다:

1. POOL 층들은 파라미터가 없다
2. CONV 층들의 파라미터는 상대적으로 작다.
3. 대부분의 파라미터들은 완전연결 층에 있다.
4. 활성값의 크기도 신경망이 깊어질수록 작아진다.

왜 합성곱을 사용하나?

완결 연결 층 대신 합성곱 층을 사용할 때 이점은 파라미터의 개수를 적게 유지할 수 있다는 점이다. 합성곱 신경망은 아래와 같은 이유를 통해 파라미터의 개수를 적게 유지할 수 있다.

1. 변수 공유 parameter sharing
2. 희소 연결 sparsity of connection

변수 공유 parameter sharing

A feature detector (such as a vertical edge detector) that is useful in one part f the image is probably useful in another part of the image.

• 변수 공유는 속성 검출기 관찰을 통해 발견되었다.
• 이미지의 특정 부분에 유용한 것이 다른 부분에도 유용하다는 것
• 즉, 동일한 필터를 이미지 전체의 다양한 부분에 동일하게, 같은 특성을 관찰하기 위해 사용할 수 있다는 것이다.
• 같은 변수들을 공유한다 = 같은 필터를 사용한다

희소 연결 sparse connection

In each layer, each output value depends only on a small number of inputs.

• 결과 행렬의 한 값은 필터의 사이즈만큼의 데이터랑만 연결되어있다.
• 필터의 범위만큼의 데이터를 제외하면, 입력 이미지의 나머지 데이터는 아무런 영향을 주지 않는다.

이 두 방법을 통해 신경망의 변수가 줄어들어 작은 훈련 세트를 갖게 되어 과대적합을 방지한다.

이동 불변

또한 합성곱 신경망은 이동 불변성을 포착하는데 용이하다.

• 특정 사진, 예를 들면 고양이 사진을 몇 픽셀 움직여도 여전히 고양이인 것처럼, 합성곱 신경망은 이러한 이동을 포착하는데 용이하다.
• 몇 픽셀을 이동한 이미지도 비슷한 특정을 갖고 있으며 동일한 결과를 갖게 되는 것
• 모든 이미지의 위치에 동일한 필터를 적용하고, 초반과 이후 층들에서도 자동으로 학습할 수 있고 이 이동 불변성을 포착할 수 있는다.

합성곱 신경망의 정리

• 합성곱과 풀링 층, 그리고 완전 연결층을 갖는 합성곱 신경망이다.

• 합성곱 신경망과 완전 연결 층은 가중치 $w$와 편향 $b$를 변수 갖는다.
• 이러한 변수들을 총해 비용함수 $J$를 계산할 수 있게 된다.
  • Cost $J = \frac{1}{m}\sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)})$
• 이 신경망을 훈련시키기 위해 경사하강법이나 모멘텀이나 RMSProp을 사용해서 비용함수를 줄인다.
• 이것이 가능하다면 효율적인 (고양이) 검출기를 만들 수 있을 것이다.