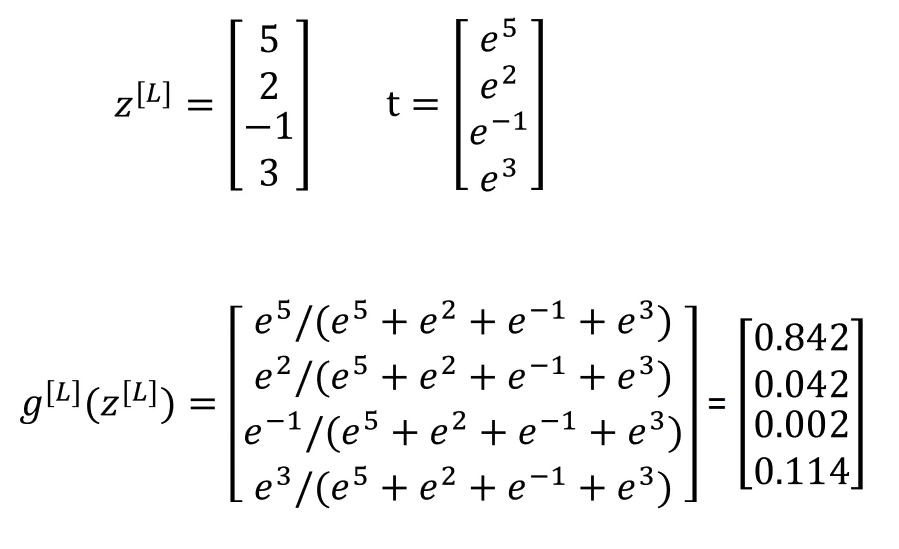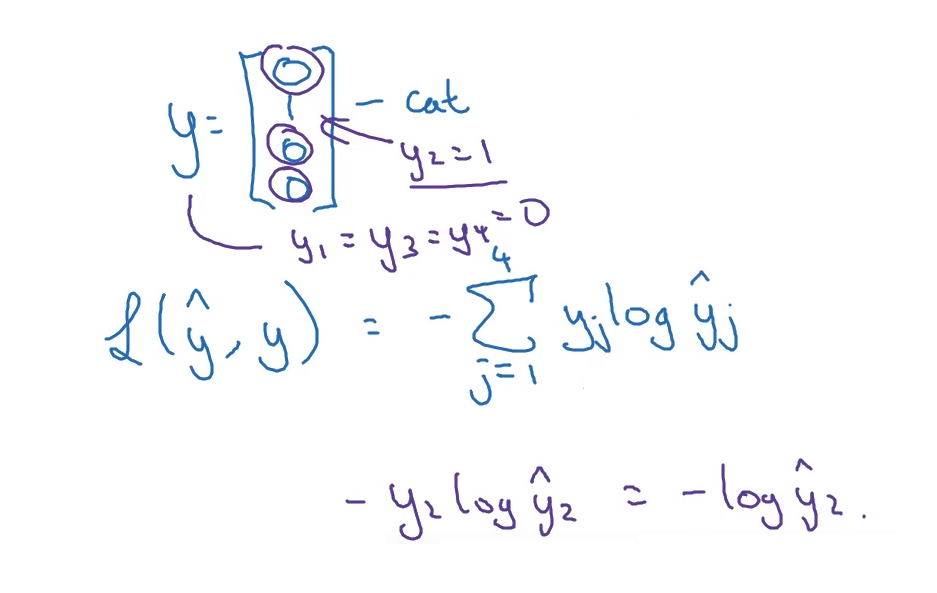11 다중 클래스 분류 및 프로그래밍 프레임워크 소개

boostcourse의 [딥러닝 2단계: 심층 신경망 성능 향상시키기] 강의를 수강 후 요약한 내용

7. 다중 클래스 분류

Softmax

• 로지스틱 회귀를 일반화한 소프트맥스 함수
• 두 개의 클래스가 아닌 여러 클래스나 C 중 하나를 인식할 때 예측에서 사용할 수 있다

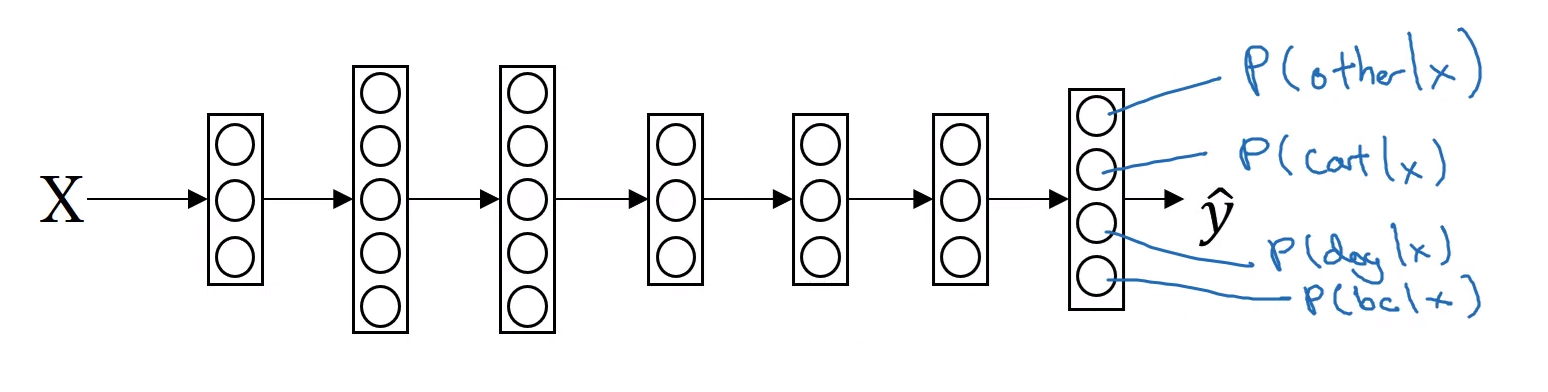
고양이, 개, 병아리 분류

• 여기서 $C$를 클래스의 갯수라고 하자
• 그렇다면 출력층이 총 4개이며, 각 클래스가 될 확률을 알려주는 신경망을 만들 수 있다.
• 모든 출력층들의 결과, 즉 $\hat{y}$의 합은 1이 되어야할 것이다.

Softmax Activation Function

• 마지막 층에서 $z$를 계산한 후, activation function이 아닌 softmax function을 통과하게 될 것이다.
• $t=e^{z^{[L]}}$ where its shape is $(4,1)$
• $a^{[L]} = \frac{e^{z^{[L]}}}{\sum_{j=1}^4 t_i}$, where its shape is $(4,1)$
  • $a_i^{[l]}=\frac{t_i}{\sum_{j=1}^4 t_i}$
• 즉, $z$값에 $e$를 취해서 임시변수 $t$값을 계산하여 정규화하 $a$를 계산하는 과정을 softmax activation function으로 요약할 수 있다.
• 이전 활성화 함수는 실수를 입력받아 실수를 결과로 출력했지만, 이 소프트맥스 활성화 함수에 특이한 점은 (4,1) 벡터를 받아 (4,1) 벡터를 출력함에 있다.

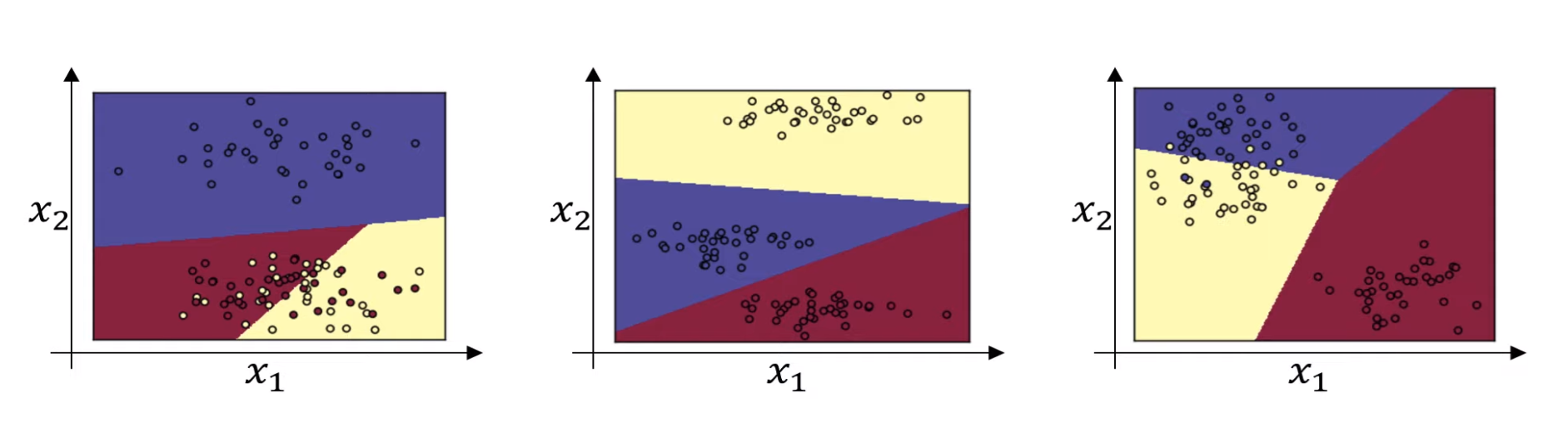
만약 은닉층이 없고 $x$를 바로 소프트맥스 함수에 적용시킨다고 하면, (클래스가 2개 이상인) 선형 기준을 갖고 있는 로지스틱 회귀의 일반적인 형태로 학습한다.

💡 만약 훨씬 복잡해진다면 비선형 형태가 될 수는 있지만, 대부분의 모델에서 중요한 것은 클래스들 사이의 경계가 선형이라는 것

Softmax Classifier 훈련

💡 Softmax regression generalizes logistic regression to $C$ classes. If $C=2$, when we apply softamx, the result is reduced to logistic regression.

손실함수 Loss Function

• 여기서 y 값에서 “정답”이 1이면, 나머지 값들이 0일 것이다.
• 그렇다면 이 값을 통해 loss값을 계산할 때 $y_i$의 합을 구할 때, 특정 $y_i$ (이 예시는 $y_2$)를 제외하면 다 0이기 때문에 결국 $y_2$를 사용하는 것과 같을 것이다.
• 그렇기에 훈련세트에 대응하는 출력값의 확률을 가장 키우는 것이 목표이다.
• 이 논리는 통계학의 최대우도추정과 유사하다 (Maximum Likelihood)

경사하강법 Back Propagation

• 정방향 전파에서는 $z$값을 계산하여 (shape은 $(4,1)$) $a$를 계산하고, 이 $a = \hat{y} \rightarrow L(\hat{y}, y)$로 손실함수를 계산했다.

• 역방향 전파에서 중요한 것은 $dz$를 계산할 때, 이 미분값이 $(C,1)$ 벡터들의 차이이기 때문에 결과도 $(C,1)$가 될 것을 기억하는 것이다.

  $dz^{[L]} = \hat{y}-y$

• 만약 tensorflow를 사용하게 된다면, 정방향 전파에 집중해도 알아서 미분 계산을 해줄 것이다.

8. 프로그래밍 프레임워크 소개

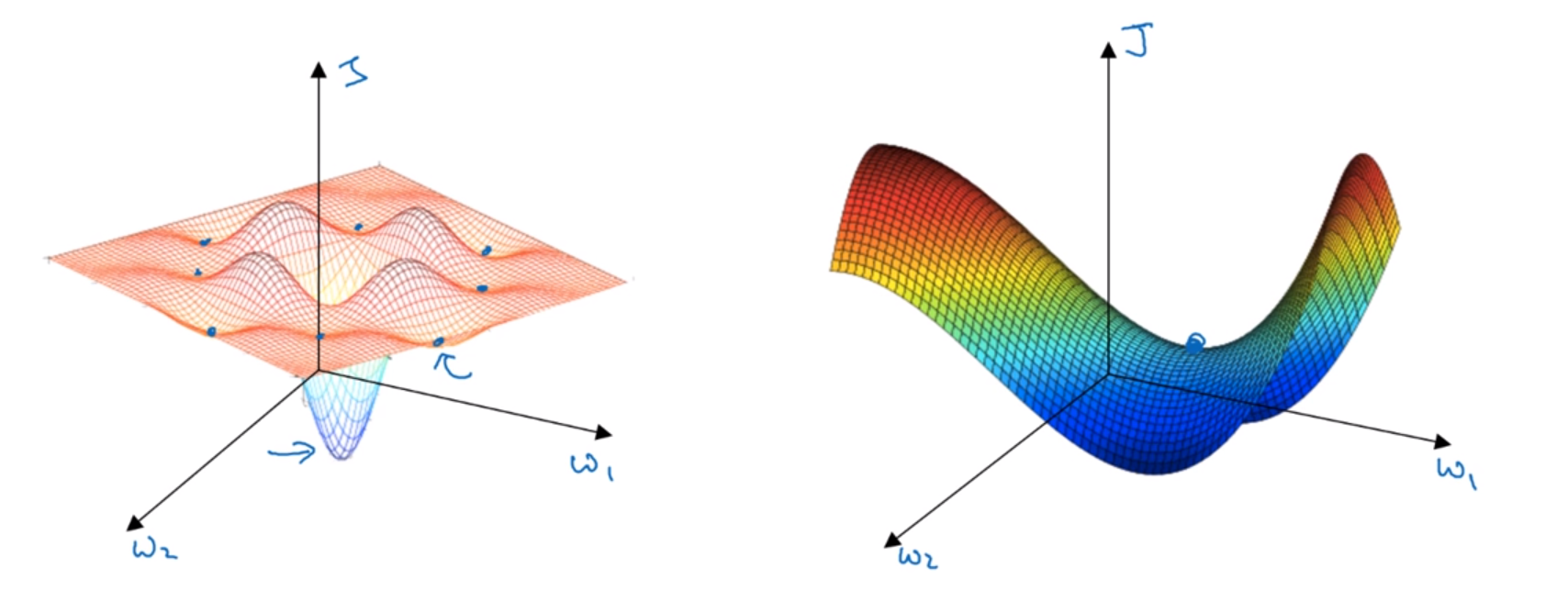
지역 최적값에 대한 문제

• 그동안 지역 최소값에 대한 문제는 왼쪽의 그림처럼 묘사되었다.
• 하지만 더 깊고 복잡한 고차원의 신경망이 다뤄지면서, 실제로는 오른쪽과 같은 형태가 더 자주 나타난다는 것을 알게되었다.

image source

• 여기서 나오는 것은 지역 최소값이 아닌 안장점(saddle point)이며, 이 안장점은 convex와 concave 형태로 이뤄져있다.
• 안정지대(plateaus), 즉 미분값이 0에 가까운 값들이 많는 부분은 학습을 느리게 하기 때문에 문제가 된다.
• 이 문제는 단순히 0에 가까운 값으로 움직이는 것이 아닌, 모멘텀이나 RMSProp, Adam 등에 알고리즘을 통해 왼쪽이나 오른쪽에 무작위로 가게 된다면 더 빠르게 이 안정지대를 벗어날 수 있을 것이다.

💡 만약 충분히 큰 고차 신경망을 학습할 때는 지역 최소값이 아닌 안정지대를 벗어날 수 있느냐가 더 많이 문제가 된다.

Tensorflow

\[J(w) = w^2 - 10w +25 = (w-5)^2\]

위 공식을 최소화하는 $w$의 값은 $5$일 것이다. 이것을 모른다는 가정을 하고 텐서플로우가 어떻게 이 식을 최소화하는지 알아보자.

• 텐서플로우는 장점 손실함수만 정의해놔도 경사하강법과 optimizer를 자동으로 해준다는 것이다.
• 텐서플로우에서 손실함수를 정의한다는 것은, 텐서플로우가 계산 그래프를 그리도록 하는 것이다.

import numpy as np
import tensorflow as tf

# w를 0으로 초기화 시켜주는 것
# 우리가 최적화하고 싶은 변수
w = tf.Variable(0, dtype=tf.float32)

# 비용함수를 정의
cost = tf.add(w**2, tf.multiply(-10,w), 25)
# cost = w**2 - 10*w + 25 로도 가능하다

# 경사하강법을 사용하여 비용함수를 최소화하는 학습 알고리즘
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

init = tf.global_variables_initializer()
session = tf.Session()
session.run(init)

# 아직 아무것도 학습시키지 않았기 때문에 결과는 여전히 0일 것이다.
print(session.run(w)) # 0.0

# 이 위의 코드는 관용적으로 쓰인다.

# 위 코드가 아닌 아래와 같은 코드를 사용하는 프로그래머들도 있다
# 같은 결과를 의미하지만, with를 사용하는 것이 파이썬을 사용할 때 오류나 예외의 경우 더 깔끔하다. 
with tf.Session() as session:
	session.run(init)
	print(session.run(w))

# 1번의 경사하강법 후의 w의 값을 계산
session.run(train)
print(session.run(w)) #0.1

# 1+1000번의 경사하강법 후의 w의 값을 계산
for i in range(1000):
	session.run(train)

# 정답인 5에 매우 가까워졌다는 것을 알 수 있다
print(session.run(w)) # 4.9999

• 이 예시에서는 $w$에 관해 고정된 함수를 최소화한다.
• 이제 학습 데이터의 역할을 하는 $x$를 정의해준다.