10 배치 정규화

boostcourse의 [딥러닝 2단계: 심층 신경망 성능 향상시키기] 강의를 수강 후 요약한 내용

배치 정규화

배치 정규화는 하이퍼파라미터 탐색을 쉽게 만들어줄 뿐만 아니라, 신경망과 하이퍼파라미터의 상관관계를 줄여준다. 즉, 더 많은 하이퍼파라미터가 잘 작동하게 되는 것이다. 또한 아주 깊은 신경망이라도 더 쉽게 학습할 수 있게 해준다.

로지스틱 회귀에서 입력값들을 정규화시켰을 때 경사하강법에 더 알맞는 값들도 바뀌게 되어 $W$와 $b$ 학습시키기 더 효과적인 모델을 만들어냈다.

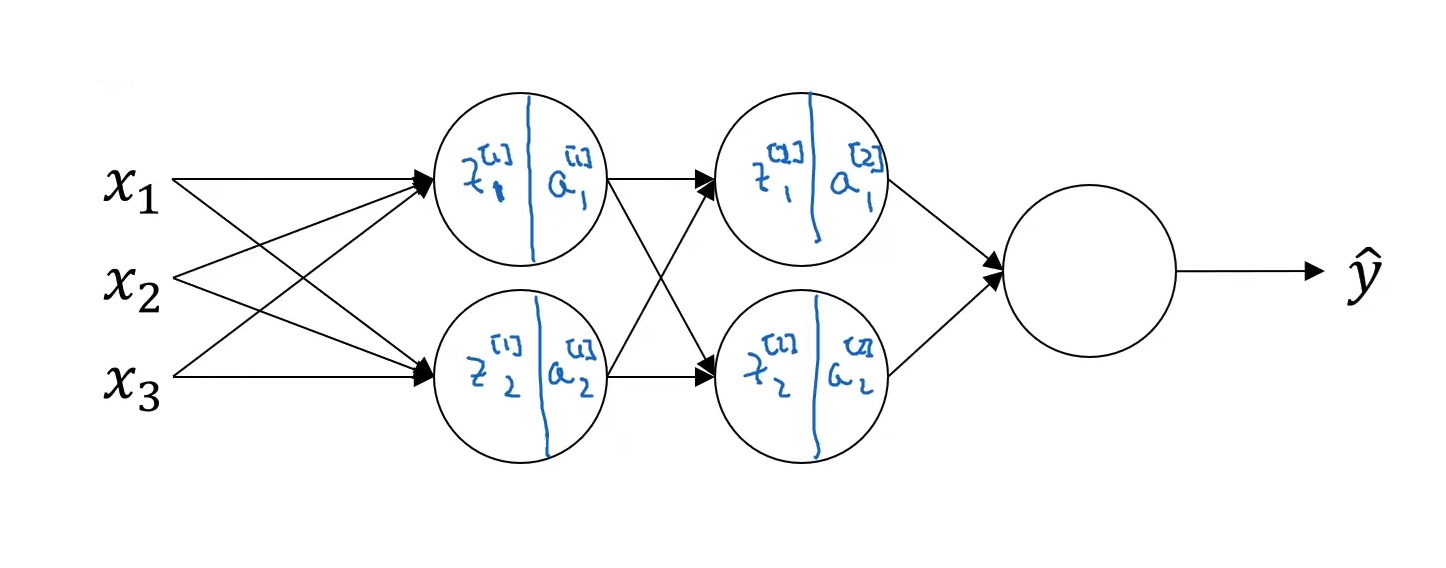
그렇다면 더 깊은 신경망에서 각 층의 평균과 분산을 정규화시키면 더 효율적일 것이다. 어떻게하면 $a^{[l]}$또는 $z^{[l]}$을 정규화시켜 $W^{[l-1]}$와 $b^{[l-1]}$를 더 빠르게 학습시킬 수 있을까?

여기서 활성화 함수에 들어가기 전의 값인 $z$를 정규화 시킬 것인지, 또는 활성값인 $a$를 정규화시킬 것인지에 대한 논란이 존재한다. 대부분의 모델들이 $z$값을 정규화 시키기 때문에 이 강의에서는 z값을 정규화 시키는 방향으로 설명할 것.

한 은닉층에서 배치 정규화의 구현

$\mu = \frac{1}{m} \sum_i{z^{(i)}}$

$\sigma^2 = \frac{1}{m} \sum_i {(z_i-\mu)^2}$

$z_{norm}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2+ \varepsilon}}$

$\tilde{z}^{(i)} = \gamma z_{norm}^{(i)} + \beta$

• 여기서 $\gamma$ and $\beta$는 모델에서 학습시킬 수 있는 변수이다. 다양한 알고리즘을 통해 신경망의 파라미터들을 업데이트 했듯이 학습시킬 수 있다.
• 또한 $\gamma$와 $\beta$를 사용하면 $\tilde{z}$의 평균을 원하는 값으로 설정할 수 있다.
• 이 값들을 어떻게 설정하냐에 따라 은닉유닛의 값들이 서로 다른 평균이나 분산을 갖게 할 수 있다.
• 그래서 신경망을 학습할 때, $z^{(i)}$가 아닌 $\tilde{z}^{(i)}$를 사용하는 것이다.

우리가 입력값을 정규화하는 것이 신경망 학습에 도움을 준다는 것을 알았고, 같은 논리를 빛 정규화를 통해 입력층에만 정규화를 시키는 것이 아닌 은닉층의 유닛들에도 정규화를 시겨 은닉 유닛들의 평균과 분산을 정규화시키는 것이다.

입력층에서의 정규화와는 다른게, 은닉 유닛들을 정규화 시킬 때는 은닉 유닛의 값의 평균과 분산이 0과 1로 고정되면 안된다는 것이다. 값들이 한 곳에 뭉쳐있기보다는 잘 분산되어있어 활성화 함수의 비선형성을 살릴 수 있도록 하는 것이 좋다.

은닉층이 표준화괸 평균과 분산을 갖되, 이것들이 학습 알고리즘에서 설정할 수 있는 변수들 $\gamma$와 $\beta$에 의해 특정한 평균과 분산을 갖을 수 있도록 조정할 수 있게 하는 것이다.

💡 배치 정규화란? 우선 평균과 분산을 $0$과 $1$로 정규화 시켜준 후, $\beta$와 $\gamma$를 통해 $0$과 $1$이 아닌 특정한 평균과 분산을 갖게 하는 것

심층 신경망에서 배치 정규화의 구현

$x$와 $w^{[1]}, b^{[1]}$를 통해 $z^{[1]}$를 계산한다.

만약 배치 정규화를 하지 않는다면 바로 활성화 함수에 넣어 $a^{[1]}$를 계산하겠지만, 만약 배치 정규화를 하게 된다면, $z^{[1]}$와 $\beta^{[1]}, \gamma^{[1]}$를 통해 $\tilde{z}^{[1]}$를 계산한 수 활성화 함수에 넣어 $a^{[1]} = g^{[1]}(\tilde{z}^{[1]})$를 계산한다.

파라미터

이제 이 알고리즘에서 사용되는 파라미터들은 아래와 같다.

• $W^{[1]}, b^{[1]}, …, W^{[l]}, b^{[l]}$
• $\beta^{[1]}, \gamma^{[1]}, …, \beta^{[l]}, \gamma^{[l]}$
  • 각 은닉 유닛 값을 조정하는데 쓰이기 때문에, $\beta$와 $\gamma$ 모두 $(n^{[l]},1)$의 차원을 갖고 있다

여기서 사용되는 $\beta$값은 모멘텀, Adam, RMSProp에서 사용되는 $\beta$랑은 관련이 없음을 주의해야한다.

경사하강법, Adam, Momentum, RMSProp 등을 통해 이 파라미터들을 업데이트할 수 있다.

배치 정규화가 $z^{[l]}$의 평균을 $0$으로 만들기 때문에 b******^******{[l]}라는 변수가 의미 없어진다. 이 변수 대신, 결과적으로 편향 변수에 영향을 주는 $\beta^{[l]}$이 그 역할을 대신하게 되는 것이다.

미니배치에서 적용

미니배치를 사용해서 배치 정규화를 할 때는, 해당 미니배치에 있는 데이터만을 이용해서 정규화를 진행한다.

For t=1 to number of mini batches :

Compute forward propagation on $X^{{t}}$

In each hidden layer, use batch normalization

• $z^{[l]} → \tilde{z}^{[l]}$

Use back propagation to compute $dW^{[l]}, d\beta^{[l]}, d\gamma^{[l]}$

Update parameters :

• $W^{[l]} := W^{[l]} - \alpha dW^{[l]}$
• $\beta^{[l]} := \beta^{[l]} - \alpha d\beta^{[l]}$
• $\gamma^{[l]} := \gamma^{[l]} - alpha d\gamma^{[l]}$

배치 정규화가 잘 작동하는 이유

이유 1 : 은닉 유닛과 입력층 모두에서 평균과 분산을 정규화하여 학습속도를 빠르게 하는 것 이유 2 : 신경망에서 깊은 층의 가중치가 이전 층들 가중치의 변화에 영향을 덜 받는다.

공변량 변화 Covariate Shift

• 만약 x의 분포가 바뀐다면 모델을 다시 학습시켜야한다.
• Covariate shift is a situation in which the distribution of the model’s input features in production changes compared to what the model has seen during training and validation. Covariate shift is a change in the distribution of the model’s inputs between training and production data. — source

• 학습 데이터의 공변량(covariates)의 분포가 테스트 데이터의 분포가 다른 상황을 의미합니다. 수학적으로 말하자면, $p(x)$는 변화하는데, $p(y

  x)$는 그대로 있는 경우를 의미합니다. — source

공변량 변화가 왜 신경망 학습에 문제가 될까?

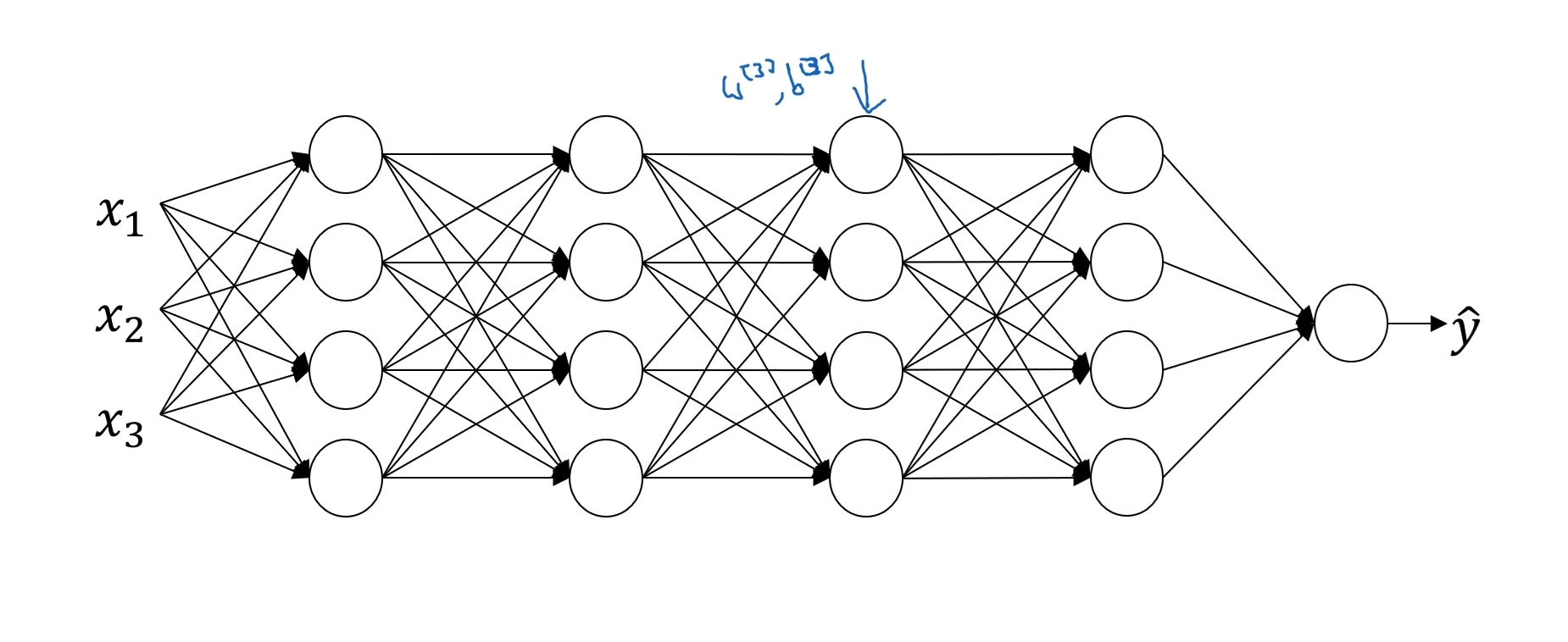
우선 세 번째 은닉층에 관점에서 신경망을 바라봐보자.

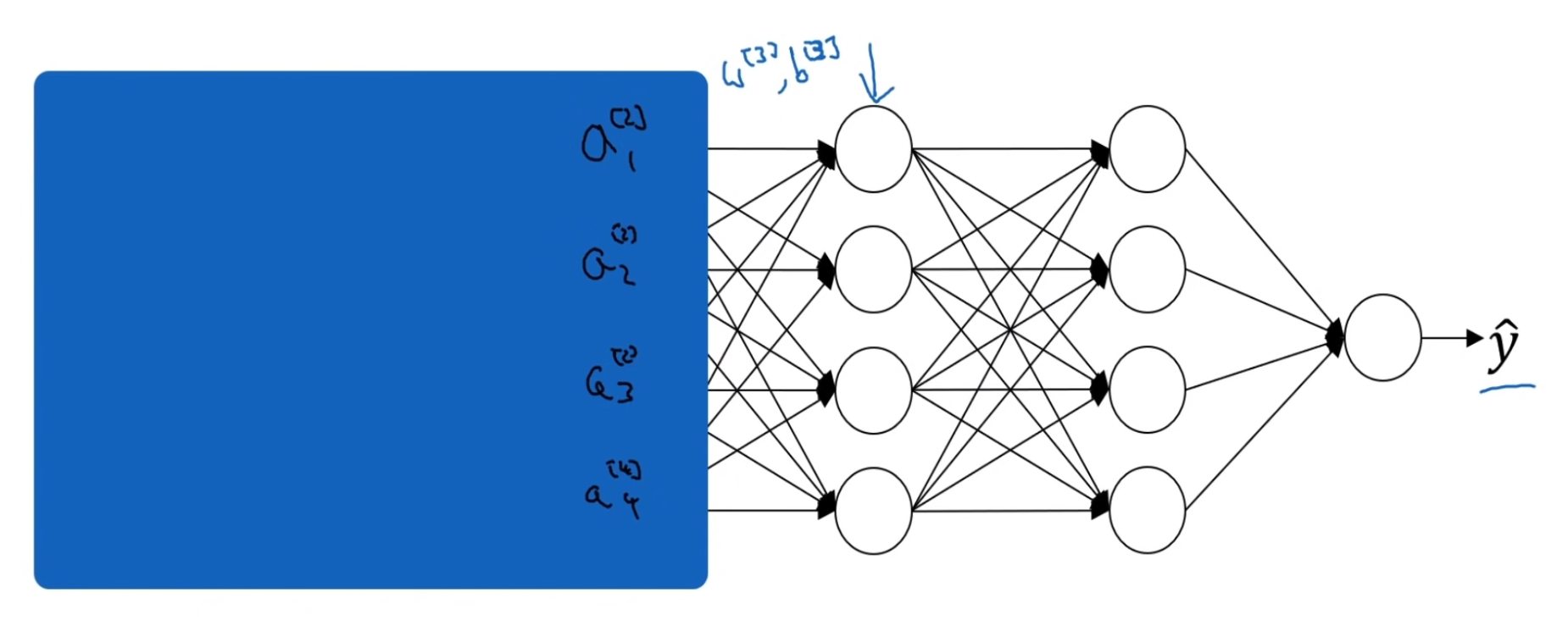
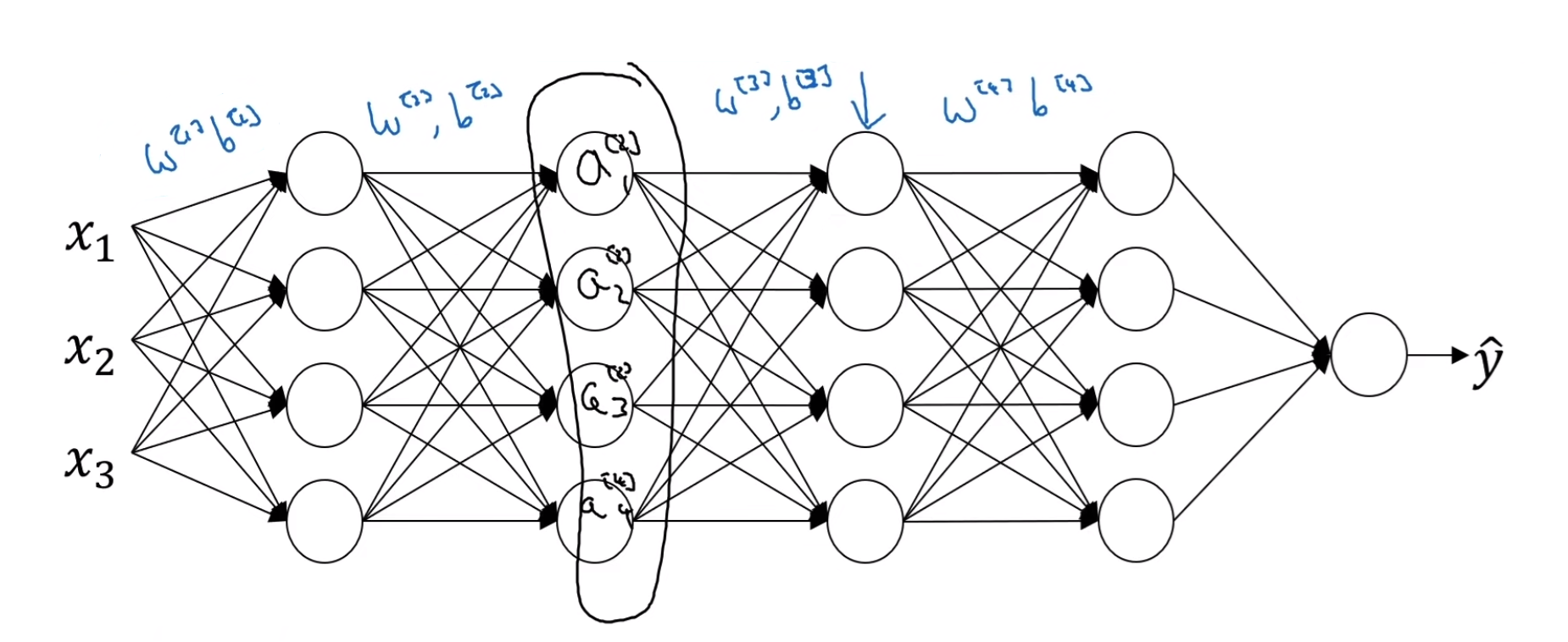
만약 첫 두 개의 은닉층을 가려놓고 본다면 두 번째 은닉층에서의 $a^{[2]}_i$값들만을 이용해서 $\hat{y}$를 구하고자 할 것이다. 이 과정에서 $W^{[3]}, b^{[3]}$와 $W^{[4]}, b^{[4]}$ 파라미터들을 이용해서 경사하강법을 진행하게 될 것이다.

하지만 첫 은닉층들을 보게 된다면, $a^{[2]}_i$의 값들은 $W^{[1]}, b^{[1]}$와 $W^{[2]}, b^{[2]}$ 파라미터들을 통해 경사하강법을 실행하여 계산된 값임을 알 수 있다. 그렇게 된다면, 계속 학습이 될수록, $a^{[2]}_i$의 값들이 계속 업데이트되면서 변할 것이다. 이 값들이 변한다면 공변량 변화의 문제가 생기게 된다.

배치 정규화는 은닉층 값들이 변화는 분포의 양을 줄여준다. 즉, 얼마나 변하던, 이들의 평균과 분산은 동일할 것을 보증한다. 앞선 레이어들에서 분포값이 변화될 때, 이후 층의 값이 받아들여서 학습하게 될 값의 분포를 제한하여 학습을 더욱 용이하게 한다.

💡 배치 정규화는 입력값이 바뀌어서 발생하는 문제들을 안정화시켜준다. 각 층의 매개변수들의 관계를 약화시켜, 각 층이 조금 더 독립되어 학습할 수 있게된다.

배치 정규화의 파라미터 정규화 효과

💡 배치 정규화는 부수적인 효과로 드롭아웃와 비슷한 약간의 regularization 효과를 갖고 있다.

• 미니배치를 사용할 경우, 각 층에서의 평균과 분산이 해당 미니배치에서 계산된다. 그렇기 때문에 전체 데이터셋을 통해 계산한 것과는 다르게 잡음 (noise)가 존재할 수 밖에 없다.
• 평균과 분산을 계산할 때 존재한 잡음이기 때문에, 배치 정규화를 할 때도 동일하게 적용되게 된다.
• 즉 드롭아웃에 곱셉 잡음이 존재하는 것처럼, 배치 정규화에서도 곱셈 잡음과 덧셈 잡음도 있다. 따라서 배치 정규화는 드롭아웃의 잡음과 비슷한 효과를 갖게 되며, 하나의 은닉층에 너무 의존하지 않도록 한다.
• 하지만 큰 미니배치 사이즈를 사용하게 된다면, 이 잡음이 줄어들어 일반화 효과가 줄어들 것이다. 따라서 정규화를 목적으로 배치 정규화를 사용하지 않지만, 학습효과를 더 올릴 수 있는 부수효과를 사용할 수 있을 것이다.
• 배치 정규화의 파라미터 정규화 효과는 단순히 부수적인 것으로, 파라미터 정규화의 효과를 바라기보다 배치 정규화를 은닉 유닛들의 값들을 정규화해서 학습 속도를 올리기 위해 사용하는 것이 더 효과적이다.

테스트 시 배치 정규화

\[\mu = \frac{1}{m} \sum_i{z^{(i)}} \\ \sigma^2 = \frac{1}{m} \sum_i {(z_i-\mu)^2} \\ z_{norm}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2+ \varepsilon}} \\ \tilde{z}^{(i)} = \gamma z_{norm}^{(i)} + \beta\]

배치 정규화를 할 때 이 $\mu$와 $\sigma^2$를 사용해서 정규화시켜준다. 하지만 모델을 테스트 할 때, 훈련을 시킬 때와는 다르게 하나의 배치를 갖고 있음으로 $\mu$와 $\sigma^2$를 계산할 수가 없다.

훈련할 때 각 미니배치에서 $\mu$ 와 $\sigma^2$을 구해야한다. 각 미니배치에서 지수가중평균을 이용해서 테스트 시 사용될 $\mu$와 $\sigma^2$의 값을 추정한다.