08 최적화 알고리즘

boostcourse의 [딥러닝 2단계: 심층 신경망 성능 향상시키기] 강의를 수강 후 요약한 내용

➀ 미니 배치 경사하강법

1차적으로 훈련을 최적화하는 것은 벡터화가 있었다. 하지만 $x$가 오백만개가 있다면 벡터화를 해도 오래걸릴 수 있다. 만약 데이터가 많아진다면, 배치 경사 하강법보다 미니 배치 경사 하강법이 훨씬 더 효과적이다.

배치 경사 하강법 : 한번에 모든 훈련 샘플에 대해 훈련 후 경사 하강 진행

미니배치 경사 하강법 : 전체 훈련 샘플을 작은 훈련 세트인 미니배치로 나눈 후 미니배치 훈련 후 경사하강을 진행한다.

50000개에 $X$와 $Y$데이터를 1000개씩 나눠서 총 $t$개의 미니배치를 만들어준다.

$X = [x^{(1)}, x^{(2)}, x^{(3)}, … , x^{(m)}]$, where $m=50000$

$X = [x^{(1)}, x^{(2)}, x^{(3)}, … , x^{(1000)} \space

\space x^{(1001)}, x^{(1002)}, … , x^{(2000)} \space

\space … \space

\space …. , x^{(m)}]$

where $x^{{1}} = x^{(1)}, x^{(2)}, x^{(3)}, … , x^{(1000)}$ as the first mini-batch of $X$

$Y = [y^{(1)}, y^{(2)}, y^{(3)}, … , y^{(m)}]$, where $m=50000$

$Y = [y^{(1)}, y^{(2)}, y^{(3)}, … , y^{(1000)} \space

\space y^{(1001)}, y^{(1002)}, … , y^{(2000)} \space

\space … \space

\space …. , y^{(m)}]$

where $y^{{1}} = y^{(1)}, y^{(2)}, y^{(3)}, … , y^{(1000)}$ as the first mini-batch of $Y$

미니 배치 하강법의 for loop

for t=1, … ,5000: ← 각 미니배치를 for loop을 통해 돌리는 것

forward prop on $x^{{t}}$

$z^{[1]} = W^{[1]}x^{{t}} + b^{[1]}$

$A^{[1]} = g^{[1]}(Z^{[1]})$

    $\vdots$

$A^{[l]} = g^{[l]}(Z^{[l]})$

$J^{{t}} = \frac{1}{1000} \sum^l_{i=1} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2*1000} \sum

w^{[l]}

_F^2$

where these $y$’s are from the mini-batch $X^{{t}}, Y^{{t}}$

Back propagation to compute gradience with respect to $J^{{t}}$

$W^{[l]} := W^{[l]} - \alpha dW^{[l]}$

$b^{[l]} := b^{[l]} -\alpha db^{[l]}$

위 for loop은 한 에포크이다. 하나의 에포크는 훈련세트를 한번 통과한 것을 의미한다.

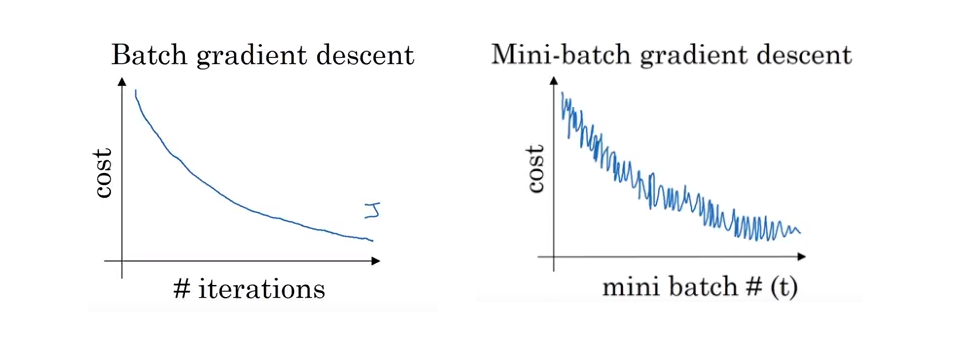
배치 경사 하강법과 미니배치 경사 하강법의 훈련

• 배치 경사 하강법에 경우, 모든 반복마다 비용함수의 값을 계속 작아져야한다. 만약 커지게 된다면 학습률이 너무 큰 것일 수도 있거나, 다른 문제가 있을 것이다.
• 미니배치 경사 하강법에 경우, 전체적이 흐름은 감소하나 약간의 노이즈가 발생할 것이다.

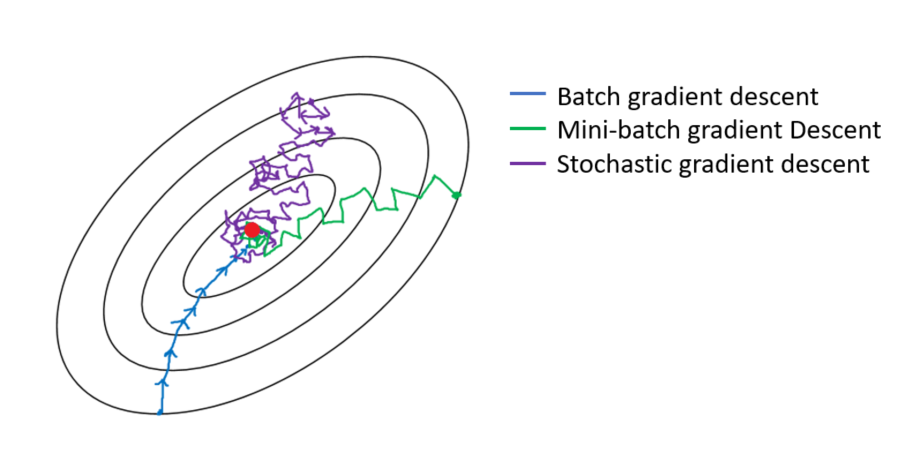
미니배치 경사 하강법에서 미니배치의 크기

두 극단적인 경우

• size = m 이라면, 배치 경사 하강법과 같다.
• size = 1 이라면, 확률적 경사하강법 (Stochastic Gradient Descent)이며, 각각의 샘플이 하나의 미니배치가 된다.
• 실제로는 미니배치의 사이즈는 1과 m의 사이가 될 것이다.

사진출처

만약 배치 경사 하강법(size=m)을 사용한다면,

• 매우 큰 훈련 세트를 모든 반복에서 진행하게 되는 것이다
• 그렇기 때문에 한 반복에서 너무 오래 걸리는 것이다

만약 확률적 경사 하강법(size=1)을 사용한다면,

• 하나의 샘플만 처리한 후 진행할 수 있어서 매우 간단하며, 노이즈도 작은 학습률을 사용해서 줄일 수 있다
• 하지만 훈련 세트의 데이터를 하나씩 돌리기 때문에, 벡터화를 통해 얻는 강점을 다 잃게 된다

그렇기 때문에 1과 m 사이에 사이즈가 가장 빠른 학습을 제공할 수 있다. 그렇게 된다면,

• 벡터화의 강점을 활용할 수 있고
• 전체 훈련 세트가 다 진행되기를 기다리지 않고 빠르게 진행할 수 있게된다

그렇다면 어떻게 적당한 값을 정할 수 있나?

• 훈련 데이터셋이 작다 : 그냥 배치 경사 하강법을 사용한다
• 만약 데이터가 크다면 : 64, 128, 256, 512 중 하나의 값이 좋다.
  • 컴퓨터 메모리의 접근 방식을 생각해보면, 2의 제곱인 값을 사용했을 때 가장 효과적이다.
  • 또한 모든 $X^{{t}}$와 $Y^{{t}}$가 CPU와 GPU 메모리에 맞는 사이즈인지를 확인해야한다. 맞지 않은 사이즈를 사용한다면 성능이 급격히 안좋아질 수 있다.

◉ 지수 가중 이동 평균

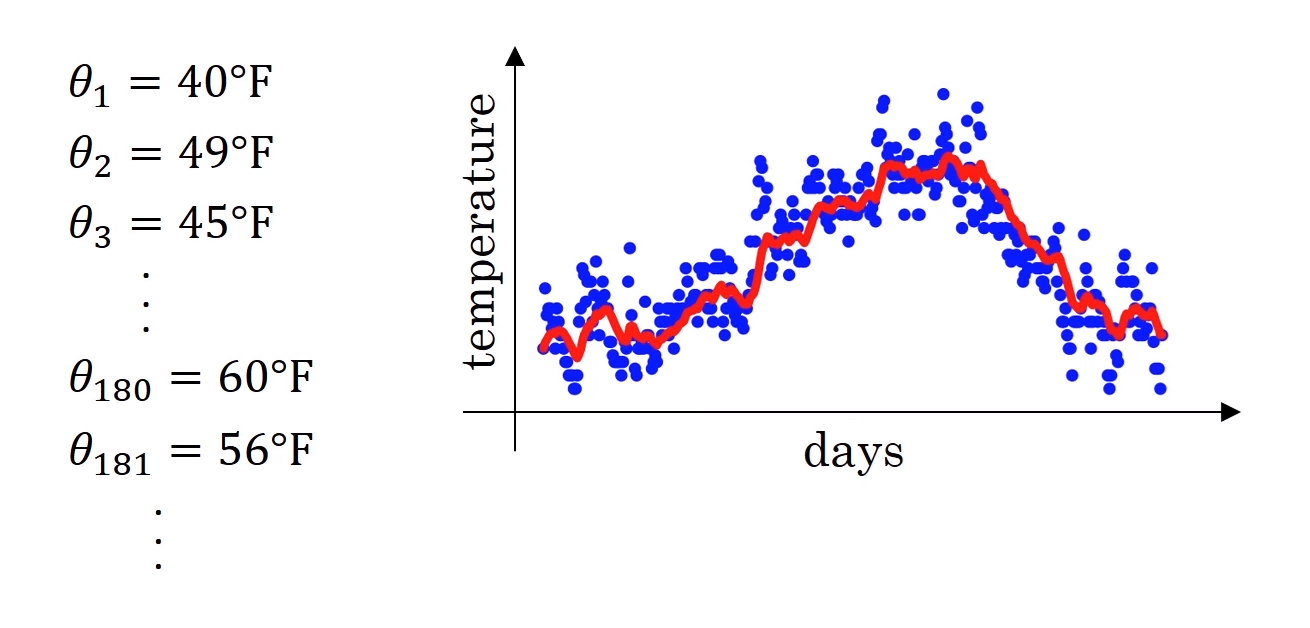
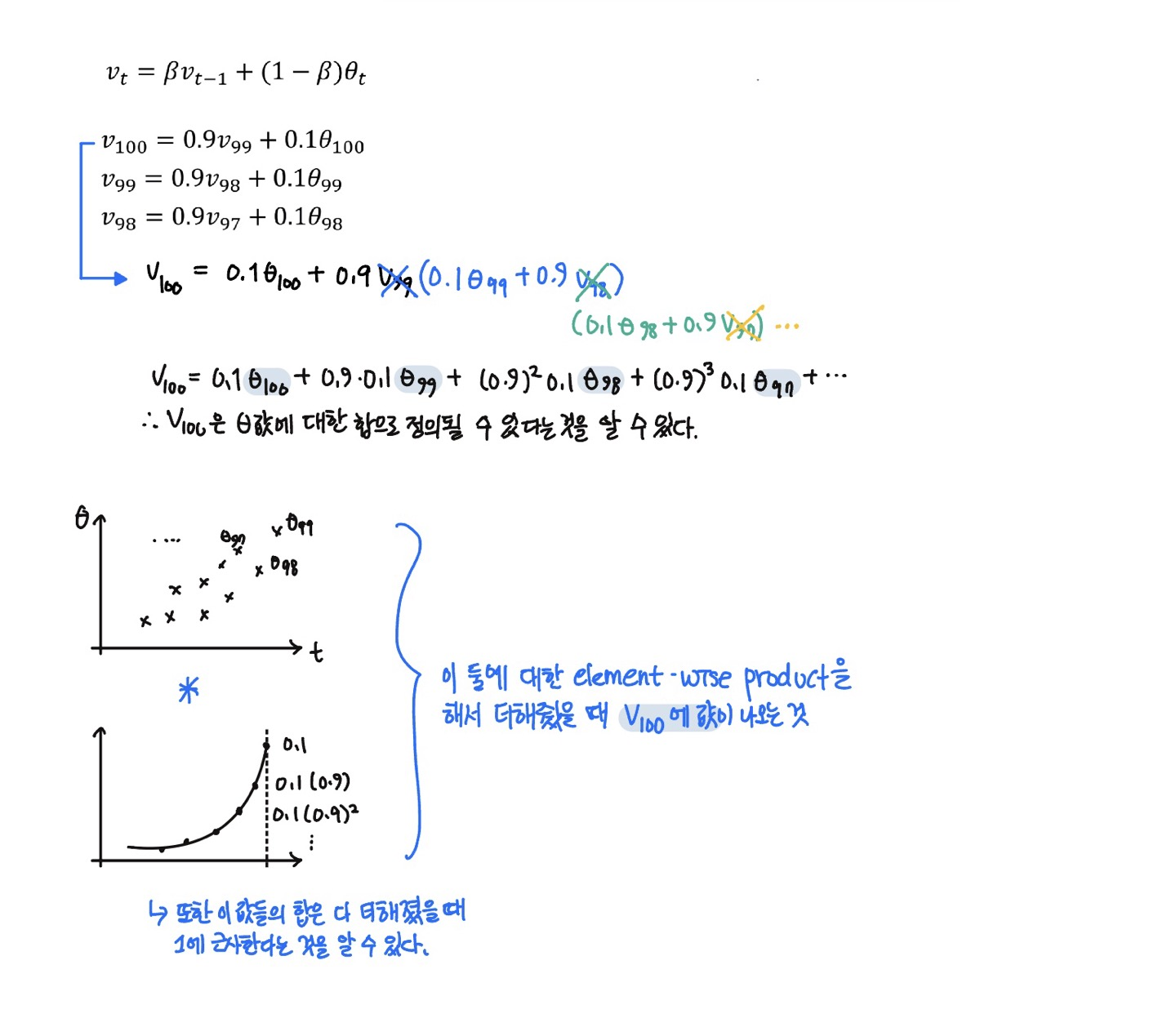
런던의 날씨 데이터다. 아래의 $\theta$들은 1월 1일부터 1년 동안 관측된 런던시의 일별 기온이며, 옆 그래프에 있는 파란 점이 이 값들이다.

만약 이 계산을 모든 데이터에 대해 하게 된다면, 일별 기온의 지수가중평균을 얻게 된다. 이 값들을 그래프로 그린 것이 저 빨간 선이다.

\[v_0 = 0 \\ v_1 = 0.9v_0 + 0.1\theta_1 \\ v_2 = 0.9v_1 + 0.1\theta_2 \\ \vdots \\ v_t = 0.9v_{t-1} + 0.1\theta_t\]

이 식을 일반화 한것이 $v_t = \beta v_{t-1} + (1-\beta)\theta_t$ 이며, 위 예시에서 $\beta=0.9$이다.

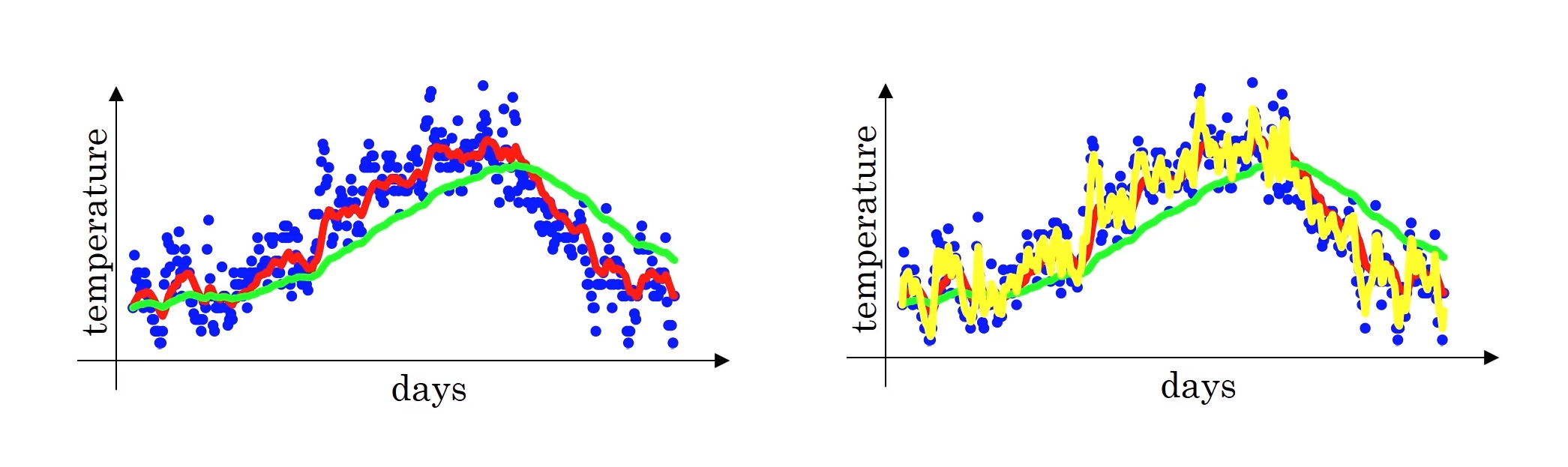
• $\beta=0.9$ 일 때, 이 값은 10일의 일별 기온의 평균이 될 것이다. (빨간색 그래프)
• $\beta = 0.98$ 일 때, 이 값은 약 50일의 일별 기온의 평균이 될 것이다. (초록색 그래프)
  • $\frac{1}{1-0.98} = 50$ 이기 때문에 그렇다.
  • 즉, $\beta$ 값이 더 클 수록 곡선이 더 부드러워지고, 이는 더 많은 날짜의 기온의 평균을 이용하기 때문에 그렇다.
  • 그러나 그렇기 때문에, 더 넓은 범위에 값들을 염두에 두고 있기 때문에, 그래프가 올바른 값에서 더 멀어진다 (right shifted).
  • 그렇기에 기온이 바뀔 경우 지수가중평균 공식이 더 느리게 적용된다. 즉 지연되는 기간이 더 큰다.
    • 이것은 $\beta$값이 커진다는 것은, 전 값, 즉 $v_{t-1}$값에 더 큰 가중치를 두고 현재 값인 $\theta_t$ 값에 더 작은 가중치를 두고 있다는 의미이기 때문이다.
    • 그렇기 때문에 현재 데이터(기온)이 변화한다면, 그 변화에 더 느리게 적응하게 되는 것이다.
• $\beta=0.5$ 일 때, 이 값은 약 2일의 일별 기온의 평균이 될 것이다. (노란색 그래프)
  • 더 적은 데이터의 평균을 구했기 때문에 더 많은 노이즈와 이상치에 더 민감한 값이 만들어진다.
  • 하지만 데이터의 변화에 더욱 민감한 데이터가 된다.

최근의 데이터에 더 많은 영향을 받는 데이터들의 평균 흐름을 계산하기 위해 지수 가중 이동 평균을 구합니다. 지수 가중 이동 평균은 최근 데이터 지점에 더 높은 가중치를 줍니다.

따라서 이 공식은 지수가중평균을 구현하기 위한 공식이다. 이 학습 알고리즘의 하이퍼파라미터를 학습함으로서 이를 통해 가장 효과적인 모델을 구현할 수 있게 한다.

위 $\beta$들 중에서는 빨강색 그래프, 즉 $\beta=0.9$ 일 때 가장 데이터를 잘 표현하는 그래프라는 것을 알 수 있다.

\[v_t = \beta v_{t-1} + (1-\beta)\theta_t\]

구현

이 식의 구현은, 단 한 줄의 코드로 구현할 수 있기 때문에 간단하다. 또한 v 값을 계속 업데이트 해 나가면서 덮어쓰기 때문에 메모리 적인 차원에서도 효율적이다.

v_theta = 0
v_theta := beta * v_theta + (1-beta)*theta[1] #덮었는 것

# for loop으로 구현한다면
v = 0
for theta_t in theta:
	v = beta * v + (1-beta)*theta_t

◉ 편향 보정

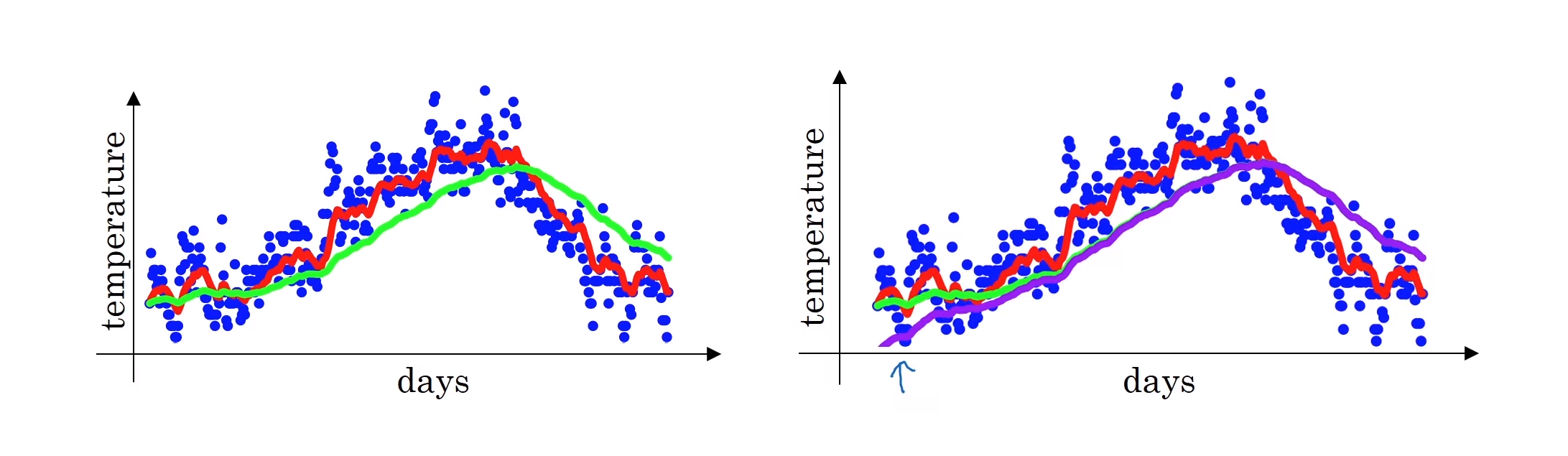
아래 왼쪽에 보이는 초록색 그래프는 위에서 보았던 $\beta=0.98$인 경우의 그래프이다. 하지만 실제로 위의 구현방법으로 구현한다면 초록색 그래프가 아닌 오른쪽에 보라색 그래프가 나오게된다. 이 보라색 그래프는 시작 지점에서의 값이 초록색 값보다 더 낮은 값에서 시작한다는 것을 알 수 있다.

낮은 값에서 시작되는 이유는 첫 $v_0$ 값이 $0$으로 초기화하기 때문이다

• $v_1 = \beta * 0 + (1-\beta)\theta_1$ 가 되기 때문에, 첫 $v_0$에 대한 부분이 없어지기 때문에 낮은 값에서 시작하게 되어 첫 번째 값을 잘 추정할 수 없게 되는 것이다.

그렇기 때문에 이를 해결하기 위해 $v_t$를 계산할 때, 편향 보정을 해주어 $1-\beta^t$로 나눠줘서 초기값에서 추정값과 실제값이 비슷할 수 있게 한다.

\[\frac{v_t}{1-\beta^t}\]

$t$가 커질수록, 편향 보정의 의미가 없어지기 때문에, 위 오른쪽 그래프에서 보이다시피, $t$가 커질수록 두 그래프들이 겹쳐지며 큰 차이가 없어진다. 그렇기에 보통 머신러닝에서 대부분 구현하지는 않지만, 이 초기 단계가 신경쓰인다면 편향보정이 도음이 될 것이다.

➁ Momentum 알고리즘

거의 항 일반 경사 하강법보다 더 빠른 성능을 가진다.

경사에 대한 지수가중평균을 계산하여 가중치를 업데이트하는 것이다.

만약 경사 하강법을 구현한다면, 아래 파랑색 그래프같이 최적값을 찾게 될 것이다. 그렇기 때문에 가로(horizontal)로는 더 빠른 학습을, 새로(vertical)로는 더 느린 학습이 되어야 더 효율적일 것이다 .

Momentum의 구현

On iteration $t$:

Compute $dW$, $db$ on current mini-batch:

$V_{dw} = \beta V_{dw} + (1-\beta) dW$

이것은 $v_\theta = \beta v_\theta + (1-\beta) \theta_t$ 와 비슷하다.

$V_{db} = \beta V_{db} + (1-\beta) db$

$w := w - \alpha V_{dw}$

$b := b - \alpha V_{db}$

where the hyperparameters are $\alpha$ and $\beta$

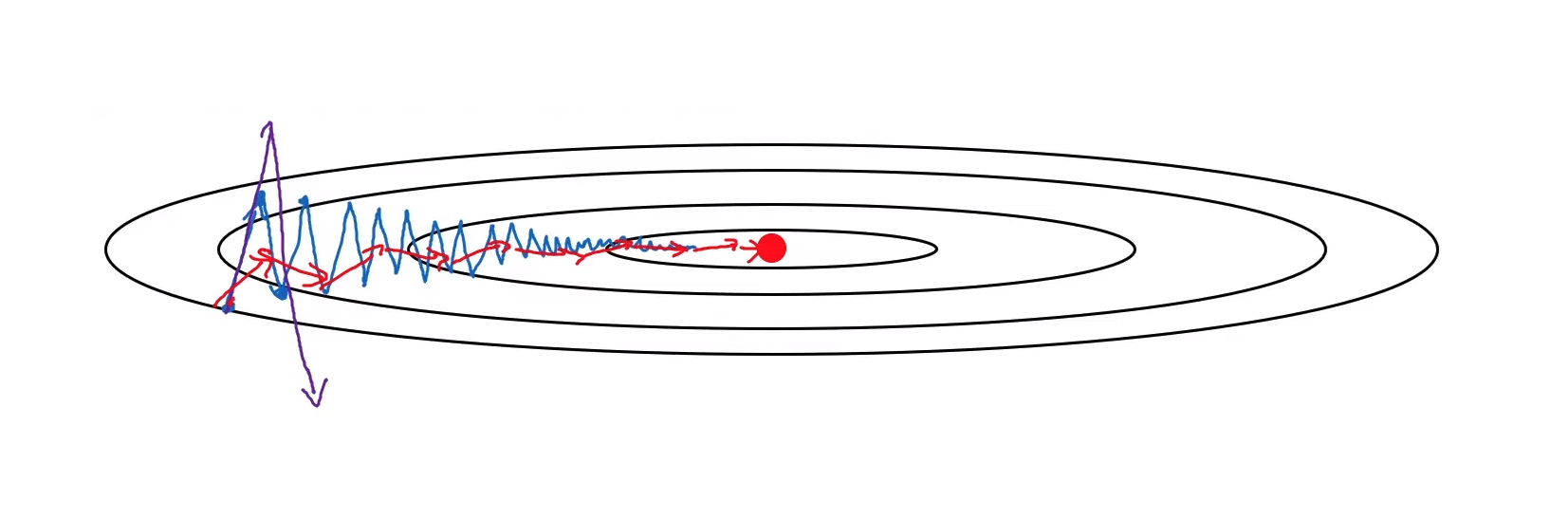
이것은 매 단계의 경사 하강 정도를 부드럽게 만들어준다.

• 수직 방향에서는 경사의 평균을 구한다면, 양수와 음수를 평균하기 때문에 평균이 0이 된다.
• 반면에 수평 방향에서는, 모든 도함수가 오른쪽을 가르키고 있기 때문에 평균은 여전히 큰 값을 가질 것이다.

그렇기 때문에 아래 빨간 그래프처럼 수직 방향에서는 훨씬 더 작은 진동이 있고, 수평 방향에서는 더 빠르게 학습하는 모습을 볼 수 있다.

➂ RMSProp (Root Means Square Propagation)

아래 경사하강법을 구현한 그래프를 다시 사용해보자. RMSProp을 설명하기 위해 $b$를 세로축, $w$를 가로축으로 설정하여 최적화시킨다.

• $w$ : 가로축은 빠르게 구현
• $b$ : 세로축은 느리게 구현

On iteration $t$:

Compute $dW$, $db$ on current mini-batch:

$S_{dw} = \beta_2 S_{dw} + (1-\beta_2) dW^2$

지수가중평균을 유지하기 위해 $v$가 아닌 $s$를 사용해준다

여기서의 제곱은 요소별 제곱을 나타냄다. 즉, 도함수의 제곱을 지수가중평균 하는 것이다.

나중에 Adam 최적화 알고리즘을 설명할 때 Momentum 구현에서 사용한 $\beta$ 와 헷갈리지 않도록 $\beta_2$를 사용해준다.

$S_{db} = \beta_2 S_{db} + (1-\beta_2) db^2$

$w := w - \alpha \frac{dW}{\sqrt{S_{dw}}}$

$b := b - \alpha \frac{db}{\sqrt{S_{db}}}$

$S$의 제곱근으로 나눠준다

그렇기에 이 $dW, db$ 값들이 0에 수렴하는 값이 되지 않게 주의해야한다.

우리가 위 구현에서 바라는 것은, $W$는 최대화되고, $b$는 최대화되는 것이다. 즉, 위 구현법에 의하면 $S_{dW}$는 최소화, $S_{db}$는 최대화하여 나눠주는 것이다.

• $w$는 작은 값으로 나눠진 큰 값을 값을 빼서 상대적으로 큰 값으로 빠르게 업데이트 된다
• $b$는 큰 값으로 나눠진 값을 빼서 상대적으로 더 작은 값으로 천천히 업데이트가 된다

미분값이 큰 곳에서는 큰 값으로 나눠주기 때문에 기존 학습률 보다 작은 값으로 업데이트 되기 때문에 더 효과적이다.

가로축과 세로축으로 $W$와 $b$로 나누는 것은 단순히 설명을 위한 것이고, 실제로는 $W$와 $b$가 고차원의 벡터이기 때문에 완전히 같지는 않다.

➃ Adam (Adaptive Moment Estimation)

Momentum과 RMSProp을 합친 최적화 알고리즘이다

초기화

$V_{dw} = 0, \space S_{dw}=0$

$V_{db}=0, \space S_{db}=0$

구현

On iteration $t$:

Compute $dW$, $db$ on current mini-batch:

#“Momentum” $\beta_1$

$V_{dw} = \beta_1 V_{dw} + (1-\beta_1) dW$ ; $V_{db} = \beta_1 V_{db} + (1-\beta_1) db$

#“RMSProp” $\beta_2$

$S_{dw} = \beta_2 S_{dw} + (1-\beta_2) dW^2$ ; $S_{db} = \beta_2 S_{db} + (1-\beta_2) db^2$

#편향 보정

$V_{dW}^{corrected} = \frac{V_{dW}}{(1-\beta_1^t)}$ ; $V_{db}^{corrected} = \frac{V_{db}}{(1-\beta_1^t)}$

$S_{dW}^{corrected} = \frac{S_{dW}}{(1-\beta_2^t)}$ ; $S_{db}^{corrected} = \frac{S_{db}}{(1-\beta_2^t)}$

$w := w - \alpha \frac{V_{dW}^{corrected}}{\sqrt{S_{dw}}}$

$b := b - \alpha \frac{V_{db}^{corrected}}{\sqrt{S_{db}}}$

하이퍼파라미터들

대부분 베타값들과 엡실론 값들은 기본값들을 활용하고, $\alpha$ 값만 보정하곤 한다.

• $\alpha :$ needs to be tuned
• $\beta_1 : 0.9$ $(dw)$
• $\beta_2 : 0.999$ $(dw^2)$
• $\varepsilon : 10^{-8}$

➄ 학습률 감쇠 Learning Rate Decay

학습 알고리즘의 성능을 높히는 방법 중 하나는, 시간에 따라천천히 학습률을 감쇠시키는 것에 있다. 하지만 학습률 감쇠는 $\alpha$를 조정하는데 도음이 되긴 하지만 모델의 성능을 최적화하기 위한 다른 방법들에 비해 우선순위가 낮다.

왜 학습률 감쇠를 구현해야하나?

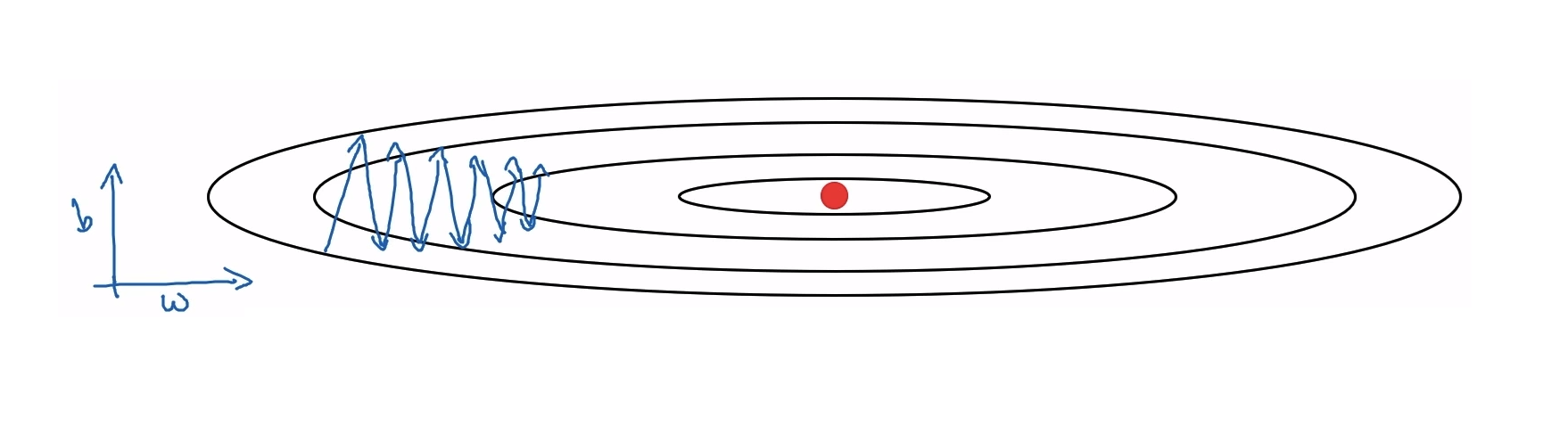
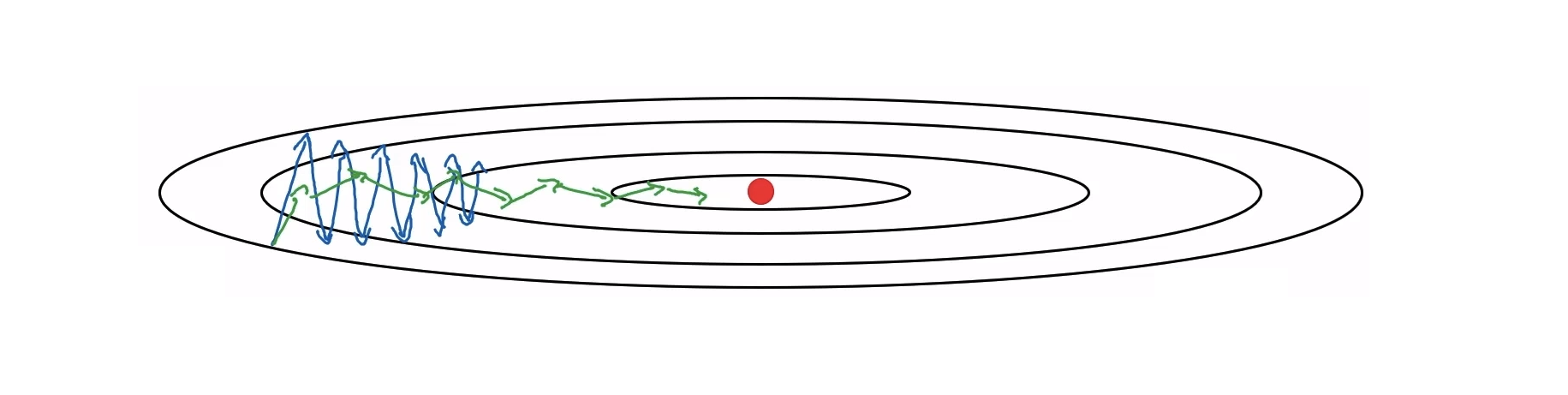
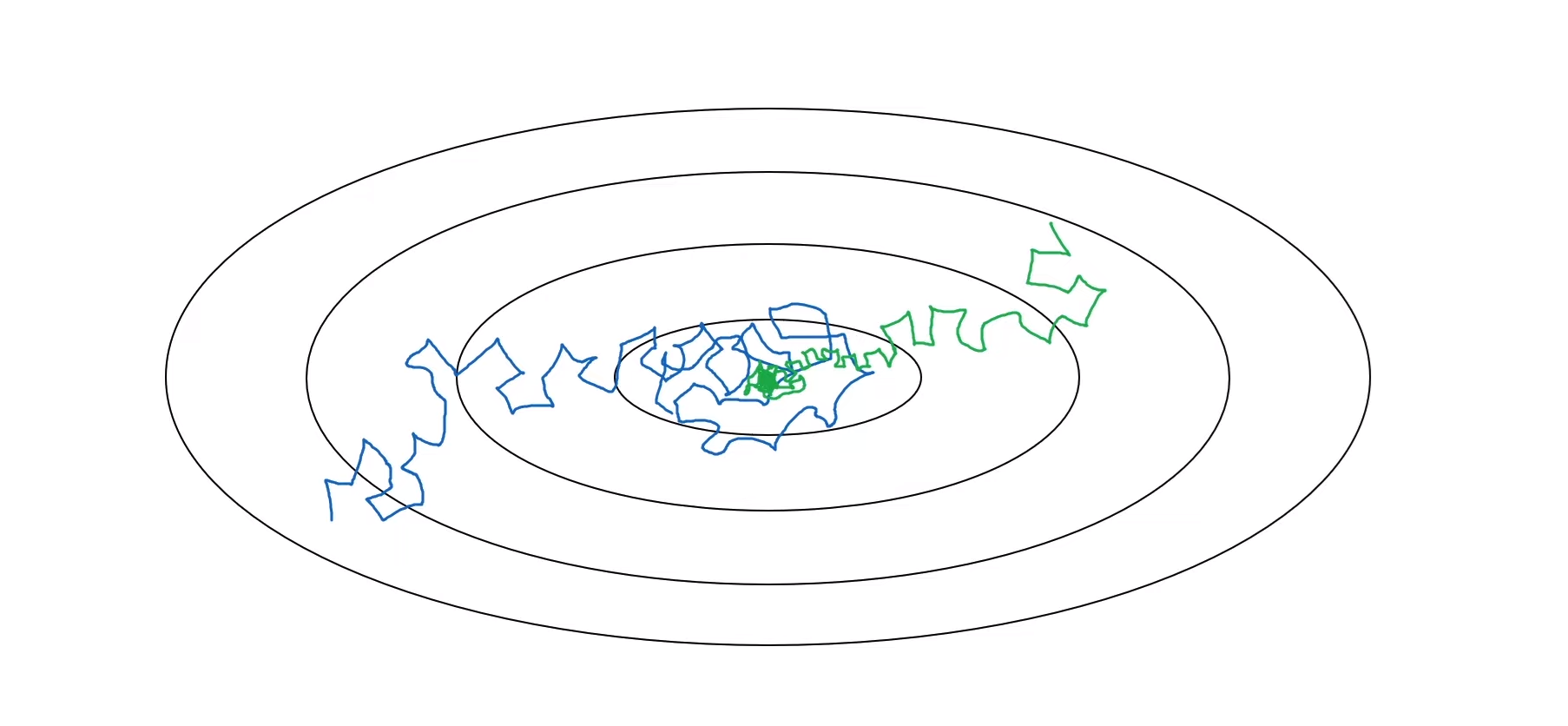
만약 작은 미니배치에서 학습한다면, $J$값이 최소값을 향해 가겠지만, 수렴하지 않고 그 최소값 근처를 배회한다. 하지만 $\alpha$값을 천천히 감소시켜준다면, 최소값에 가까워질수록 더 좁은 범위에서 배회할 것이다. 즉, 초반에는 더 큰 학습률로 학습시키고, 최소값에 가까워질수록 더 촘촘하게 학습할 수 있게 하는 것이다.

파랑색 그래프가 일반 미니배치 경사 하강법이며, 초록색 그래프가 학습률 감쇠를 적용한 모양이다.

• 1 epoch : 1 pass through the data

다양한 학습률 감쇠 방법

• $\alpha = \frac{1}{1+ decay\space rate * epoch\space number } \alpha_0$
• Exponential Decay : $\alpha = 0.95^{epoch \space number} \alpha_0$
• $\alpha = \frac{k}{\sqrt{epoch \space number}} \alpha_0$ or $\alpha = \frac{k}{\sqrt{t}} \alpha_0$
• Discrete Staircase : 각 단계별로 $\alpha$ 를 다르게 설정하는 것
• Manual Decay : 각 학습률을 직접 조정하는 것 (적은 수의 모델들을 훈련시킬 때 가끔 사용한다)